Feladat: 1964. évi Kürschák matematikaverseny 1. feladata Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Corradi Gábor ,  Gerencsér László ,  Laczkovich Miklós ,  Lovász László ,  Makai Endre 
Füzet: 1965/március, 98 - 101. oldal  PDF  |  MathML 
Témakör(ök): Szabályos sokszög alapú gúlák, Tetraéderek, Szabályos tetraéder, Egyenlő szárú háromszögek geometriája, Háromszögek hasonlósága, Magasságvonal, Súlyvonal, Súlypont, Tengely körüli forgatás, Térbeli szimmetrikus alakzatok, Síkra vonatkozó tükrözés, Négyszög alapú gúlák, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):Feladatok: 1965/március: 1964. évi Kürschák matematikaverseny 1. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Ha a szabályos ABC▵ mentén összeillesztjük az egybevágó ABCD, ABCE gúlákat (1. ábra), a D, E csúcsok a háromszög síkjára a háromszög S középpontjában emelt merőlegesen helyezkednek el. Az összeillesztéssel keletkező test eszerint nemcsak az ABC síkra, hanem pl. az ADE síkra is szimmetrikus. E szimmetriákból következik, hogy a D, E csúcsokból az AB élre, valamint a B, C csúcsokból az AD egyenesre bocsátott merőlegesek egyenlők, s hogy közös F és G talppontjuk van. Eszerint a DFE∢ az AB él mentén, a BGC∢ pedig az AD él mentén csatlakozó lapok szögét méri. Minthogy e szögek a feltevés szerint egyenlők, a DFE, BGC háromszögek hasonlók, hiszen egyenlő szárúak és szárszögük ugyanakkora.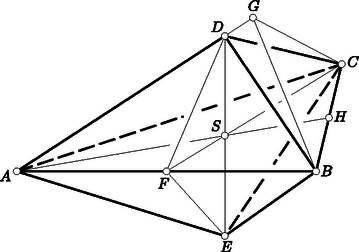

 
 

1. ábra
 

A hasonlóságból a megfelelő oldalak arányára
DE:BC=DF:BG
következik. A jobb oldali szakaszok az ABD▵ magasságai, s ezért fordítva aránylanak, mint a megfelelő oldalak:
DF:BG=AD:AB.
Minthogy BC=AB, az aránypárok egybevetéséből DE=AD következik, tehát az is, hogy az ADE▵ szabályos, és így hasonló az ABC▵-höz. Ebből a hasonlóságból az oldalak és magasságok arányára
DE:BC=AS:AH
adódik. Minthogy az S súlypont harmadolja az AH súlyvonalat, az utolsó arány értéke 2/3. Ez tehát egyben a DE:BC arány keresett értéke is.
 
Megjegyzés. Feladatunk abból a feltételezésből indul ki, hogy van olyan test, amelyre a feladat követelménye teljesül, azaz lapszögei mind egyenlők. Rámutatunk itt arra, hogy ez valóban igaz, mégpedig éppen úgy jutunk hozzá, hogy a DE:BE arány értékét a megoldásban talált 2/3-nak választjuk, azaz a szabályos ABC▵ középpontjában a háromszög síkjára emelt merőlegesen mindkét irányban a háromszög oldalának harmadát mérjük fel, s az így kapott D, E csúcsok által meghatározott testet tekintjük. Ennek az állításnak a helyessége megoldásunk gondolatmenetének megfordítása útján látható be.
A szerkesztés következménye ugyanis, hogy a megoldásbeli utolsó aránypár teljesül, s ebből következik, hogy az ADE▵ és ABC▵ hasonló, hogy tehát az ADE▵, is szabályos. Eszerint AD=DE, és a középső aránypár jobb oldalán álló arány értéke 2/3. Ennyi tehát a bal oldali arány értéke is, s ezért az első aránypár is helyes. Ebből viszont az egyenlő szárú DFE▵ és BGC▵ hasonlósága adódik, s ezek megfelelő szögeinek egyenlősége miatt a szerkesztett test lapszögei valóban egyenlők.
A szóban forgó testhez a legegyszerűbben talán úgy juthatunk el, hogy egy szabályos ADE▵-et DE oldala körül mindkét irányban 120∘-kal elforgatunk, s az így adódó három háromszög által kifeszített testet tekintjük. Ez közvetlenül adódik a fentiekből.
 
II. megoldás. Az 1. ábra jelöléseit használjuk, és abból indulunk ki, hogy az összeillesztéssel keletkező test az ABC síkra és az ADE síkra is szimmetrikus. Eszerint ez a két sík az AB élű és az AD élű lapszöget felezi, s e lapszögek feltételezett egyenlősége miatt a két sík mindegyike ugyanakkora lapszöget alkot az ABD síkkal.
Tükrözzünk a BAD∢ szögfelezőjében a szög síkjára merőlegesen emelt síkra. E tükrözéskor az AB és AD szárak is, s az imént említett lapszögek egyenlősége miatt az ABC és ADE síkok is helyet cserélnek. Ezért AS metszésvonaluk helyben marad, és a szimmetrikus BAS∢ és DAS∢ egyenlő. Ha tehát a DE szakaszt az AS tengely körül 90∘-kal elforgatjuk, D és ugyanúgy E az AB és AC élre jut, s ezért DE egyenlő az ABC▵-et átvágó, AS-re merőleges B1SC1 szakasszal (2. ábra). Minthogy pedig S az ABC▵ súlypontja, s ez A-tól 2/3-szor akkora távolságra van, mint a BC oldal felezőpontja, a keresett arány
DE:BC=B1C1:BC=23.

 
 

2. ábra
 

III. megoldás. Tekintsük az összeillesztéssel keletkező bipiramis A csúcsú, négyélű szögletét. Ezt a szögletet négy egyenlő szögtartomány határolja, amelyek a feltevés szerint egyenlő lapszögeket alkotva csatlakoznak egymáshoz. Eszerint ez négyoldalú szabályos szöglet, azaz olyan, mint a négyoldalú szabályos gúla csúcsánál elhelyezkedő, amely a gúla tengelye körül 90∘-kal elforgatva önmagát fedi.
Ha tehát a bipiramis DSE tengelyét az A csúcsú szöglet AS tengelye körül 90∘-kal elforgatjuk, akkor az előző megoldásban említett B1C1, szakaszhoz jutunk. Ebből a feladat kérdésére adandó válasz már ugyanúgy következik.
 
Megjegyzés. Utolsó megoldásunk nemcsak azért rövid, mert az előzőre hivatkozott, hanem azért is, mert a szögletekre vonatkozó ismeretekre támaszkodott. Mielőtt ezeket részleteznők, néhány elnevezést említünk meg.
Tekintsünk egy poliédert, annak egyik csúcsát és mindazokat az ebből a csúcsból kiinduló félegyeneseket, amelyeknek egy kezdőszakasza a poliéderhez tartozik. E félegyenesek pontjai együttesen egy végtelenbe nyúló alakzatot alkotnak, amelyet a poliéder szögletének nevezünk. A szöglet legtöbbször végtelenbe nyúló gúla. A szögletet határoló szögtartományok a szöglet oldalai, s a csatlakozó oldalak által alkotott lapszögek a szöglet szögei.
Egy szöglet akkor szabályos, ha minden oldala és minden szöge ugyanakkora. Bebizonyítjuk, hogy a szabályos n-oldalú szögletnek van tengelye, amely körül 360∘/n szöggel elforgatva a szöglet újból ugyanabba a helyzetbe jut. Megoldásunk ezt használta fel az n=4 esetben.
 
 

3. ábra
 

Tekintsük az OA1, OA2, ..., OAn élű, n-oldalú szabályos szögletet, (3. ábra). Az A1OA2∢ síkjára az OF1 szögfelező mentén merőleges síkot emelünk. Ezt a síkot az OA2 élű lapszöget felező sík a t egyenesben metszi. A szabályosság miatt A1OA2∢=A2OA3∢, s ezért e szögek a lapszögüket felező A2Ot síkra vonatkozólag szimmetrikusan helyezkednek el. Ebből a szimmetriából következik, hogy az F1Ot sík tükörképe az A2OA3∢ síkját annak OF2 szögfelezőjében metszi, s hogy OF1 és OF2 ugyanakkora szöget zár be a t egyenessel. Ha tehát a szögletet t körül az F1Ot, F2Ot síkok hajlásszögével elforgatjuk, akkor az A1OA2 oldal fedi az A2OA3 oldalt. Minthogy pedig a szabályos szöglet szögei egyenlők, az elforgatott A2OA3 oldal az A3OA4 síkba kerül, és a szöglet oldalainak egyenlősége miatt az OA3 él az OA4 helyzetbe jut. Ugyanígy következtethetünk azonban tovább, és megállapíthatjuk, hogy valamennyi oldal és él a rákövetkezőnek a helyét foglalja el. Ha tehát ezt az elforgatást n-szer megismételjük, mindegyik az n-edik rákövetkezőt, azaz önmagát fedi. Eszerint ez az n-szeres elforgatás 360∘-os, és egy elforgatás valóban ennek n-edrésze.
Ha n páros, legyen n=2k. Ekkor a k-szoros elforgatás 180∘-os, tehát a tengelyre vonatkozó tükrözést jelent. Ebben az esetben kimondhatjuk tehát, hogy a tengely az átellenes élek szögét felezi. Megoldásunk az n=4 esetben ezt is felhasználta.