Feladat: 1963. évi Kürschák matematikaverseny 3. feladata Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Fazekas Patrik ,  Gerencsér László ,  Lukovics Edit ,  Máté Attila 
Füzet: 1964/április, 150 - 153. oldal  PDF  |  MathML 
Témakör(ök): Háromszögek nevezetes tételei, Súlyvonal, Körülírt kör, Geometriai egyenlőtlenségek, Fizikai jellegű feladatok, Háromszög-egyenlőtlenség alkalmazásai, Egyenlő szárú háromszögek geometriája, Magasságvonal, Számtani közép, Kvadratikus közép, Tetraéderek, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):Feladatok: 1964/április: 1963. évi Kürschák matematikaverseny 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Ha az ABC△ nem tompaszögű, akkor (a belsejében vagy a határán) tartalmazza a köréírt kör O középpontját. Ezért az S súlypont által meghatározott SAB, SBC, SCA háromszögek közül legalább az egyik szintén tartalmazza az O pontot. Legyen az SAB△ ilyen (4. ábra).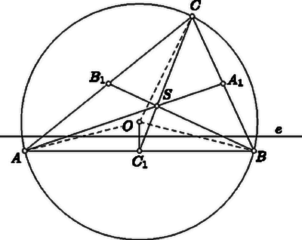

 
 
4. ábra
 

Minthogy az SAB△ tartalmazza az OAB△-et,
SA+SB≥OA+OB,
és az egyenlőség csak akkor teljesülhet, ha O és S azonos. Eszerint az sa=AA1, sb=BB1 súlyvonalakra és a körülírt kör r sugarára
23sa+23sb≥2r,
vagyis
sa+sb≥3r.

Ha O azonos C1-gyel, akkor nyilván CO=CC1. Ha azonban O nem azonos C1-gyel, akkor az OC1 szakaszt merőlegesen felező e egyenes belevág a háromszögbe, tehát a vele párhuzamos AB szakaszt elválasztja a C csúcstól. Eszerint C és O ugyanabban az e egyenes által határolt félsíkban van, s ezért a C pont az e egyenesre vonatkozólag szimmetrikusan elhelyezkedő O, C1 pontok közül O-hoz van közelebb. A CC1=sc, és CO=r szakaszokra ezek szerint
sc≥r
mindig teljesül, és egyenlőség csak akkor áll fenn, ha O és C1 azonos:
Egyenlőtlenségeinket összeadva
sa+sb+sc≥4r
adódik, de itt az egyenlőség soha sem teljesülhet, mert egyszerre nem teljesülhet mind a két összeadott egyenlőtlenségben, hiszen O nem lehet az egymástól különböző S, C1 pontok mindegyikével azonos.
 

Megjegyzések. 1. Nem hagyható el a feladatnak az a megszorítása, hogy a háromszög nem tompaszögű. Bármilyen csekély túllépést engednénk is meg, 90∘ fölé, a feladat állítása már nem volna helyes. Bebizonyítjuk, hogy ez valóban így van.
Induljunk ki tehát egy tetszőlegesen megadott ABC∢>90∘ szögből. Messe az AB=c szakasz felezőmerőlegese a BC szárra B-ben emelt merőlegest az O1 pontban (5. ábra). A BC száron úgy választjuk meg a C pontot, hogy a BC=a távolságra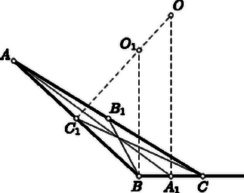
a+c≤2⋅BO1
teljesüljön. Az ABC△ köré írt kör sugarára
r=BO>A1O>BO1,
hiszen a két utolsó szakasz ugyanannak a szögnek párhuzamos szelője, és BO1 van a szög csúcsához közelebb.
 
 
5. ábra
 

Az ABC△ súlyvonalaira az ABA1, BC1B1, CBC1 háromszögek egyenlőtlenségei alapján
sa<a2+c,sb<a2+c2,sc<a+c2.
Ezek szerint
sa+sb+sc<2(a+c)<4⋅BO1<4r.

 

2. Bebizonyítjuk, hogy akkor sem volna helyes a feladat állítása, ha benne 4 helyett valamely 4-nél bármi csekéllyel is nagyobb szám állna.
Egy 2d alapú, m magasságú egyenlőszárú háromszög (6. ábra) súlyvonalaira az AA1D△-re vonatkozó egyenlőtlenség felhasználásával
sa=sb<m2+32d,sc=m,sa+sb+sc<2m+3d.


A körülírt kör sugarára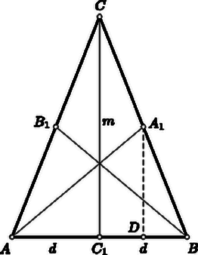
r>m2,
hiszen az m magasságot a kör tartalmazza. Ezek szerint
sa+sb+sc<(4+6dm)r.
Ha λ egy tetszőleges, 4-nél nagyobb szám, m rögzítése után d megválasztható olyan kicsire, hogy
4+6dm<λ
teljesüljön. Az így adódó háromszögre a fentiek szerint
sa+sb+sc<λr.

 
 
6. ábra
 

3. A feladat arról szólt, hogy a súlyvonalak összege a körülírt kör sugarának legalább hányszorosa. Bebizonyítjuk most, hogy legfeljebb 4,5-szöröse, és itt a háromszöget illetően semmiféle megszorítást sem teszünk. Szabályos háromszög esetében a vizsgált arány éppen 4,5. Meglepő talán a nem tompaszögű háromszögekre érvényes viszonylag szűk (4, 4,5) értékköz.
Tekintsük a sík egy P pontjának az ABC△ csúcsaitól mért távolságait. Ezek számtani közepét a(P), négyzetes közepüket pedig q(P) jelöli. Ismeretes, hogy a(P)≤q(P).
Bizonyításunk arra épül, hogy q(P)≥q(S). Ha az A, B, C pontokba egységnyi tömegeket helyezünk, akkor 3[q(P)]2 e tömegrendszer tehetetlenségi nyomatéka a síkot a P pontban merőlegesen döfő egyenesre vonatkozólag. Az imént kimondott egyenlőtlenség következik tehát abból, hogy párhuzamos tengelyek közül a súlyponton áthaladó tengelyre vonatkozó tehetetlenségi nyomaték a legkisebb.
Egyenlőtlenségünket fizikai ismeretekre való hivatkozás nélkül akarva bebizonyítani bevezetjük az
SA→=a,SB→=b,SC→=c,SP→=p
vektorokat (lásd pl. Matematikai Versenytételek, II. rész, 26‐30. o. és 69. o.). Felhasználjuk azt, hogy
a+b+c=0.
Az egyenlőtlenségünkben szereplő értékekre
3[q(S)]2=a2+b2+c2,3[q(P)]2=(a-p)2+(b-p)2+(c-p)2==(a2+b2+  c2)-2p(a+b+c)+3p2==3[q(S)]2+3p2≥3[q(S)]2.
Ezzel a q(P)≥q(S) egyenlőtlenség bizonyítást nyert, de ebből eredeti állításunk is nyomban következik:
sa+sb+sc=92a(S)≤92q(S)≤92q(O)=92r.

 

4. Megemlítjük, de nem részletezzük, hogy a tetraéder súlyvonalainak összege a körülírt gömb sugarának legfeljebb 16/3-szorosa, s hogy ez ugyanúgy bizonyítható, ahogyan a megfelelő síkbeli állítást éppen bebizonyítottuk. Ha feladatunk állításának térbeli megfelelőjét keressük, valamilyen megszorítást kell tennünk a tetraéderre vonatkozólag, annak megfelelően, hogy a feladat csak nem tompaszögű háromszögekről szólt. Azok a háromszögek nem tompaszögűek, amelyek tartalmazzák a köréjük írt kör középpontját. Érthető tehát, hogy azokról a tetraéderekről szólunk, amelyek tartalmazzák a köréjük írt gömb középpontját, azonban csak bizonyítás nélkül említjük meg, hogy az ilyen tetraéderek súlyvonalainak összege a körülírt gömb sugarának 4-szeresénél nagyobb, és itt 4 helyébe nagyobb számot írva már helytelen állításhoz jutunk.