Kezdőlap


Feladat:	1963. évi Kürschák matematikaverseny 2. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Fazekas Patrik , Gerencsér László , Lukovics Edit , Máté Attila
Füzet:	1964/április, 148 - 150. oldal		PDF \| MathML
Témakör(ök):	Trigonometrikus függvények, Trigonometriai azonosságok, Trigonometrikus egyenlőtlenségek, Geometriai egyenlőtlenségek, Nevezetes azonosságok, Pont körüli forgatás, Síkbeli szimmetrikus alakzatok, Mértani közép, Kvadratikus közép, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):	Feladatok: 1964/április: 1963. évi Kürschák matematikaverseny 2. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. A baloldali szorzat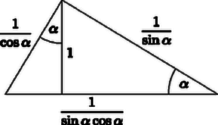

\begin{matrix} 1 + \frac{1}{sin α} + \frac{1}{cos α} + \frac{2}{sin 2 α} \end{matrix}

alakban írható, hiszen

sin α cos α = \frac{1}{2} sin 2 α

. Minthogy egy szög szinusza és koszinusza

1

-nél nagyobb nem lehet, a felírt összeg második és harmadik tagja legalább

1

, utolsó tagja pedig legalább

2

. A teljes összeg értéke tehát legalább

5

. Az összeg azonban nem lehet

5

, mert a két középső tag nem lehet egyszerre

1

, hiszen

sin α = 1

és

cos α = 1

egyszerre nem teljesülhet. Az összeg értéke eszerint

5

-nél nagyobb.

II. megoldás. Egy

α

szögű

1

magasságú derékszögű háromszöget tekintünk (2. ábra) A szögfüggvények értelmezéséből következik, hogy e háromszög befogói és átfogója

\begin{matrix} a = \frac{1}{cos α}, b = \frac{1}{sin α}, c = \frac{1}{sin α cos α} . \end{matrix}

Feladatunk

a + b + c > 4

bizonyítását kívánja. Ez nyomban következik abból, hogy

a + b > c

és

c \geq 2

, hiszen a derékszögű háromszög magassága az átfogónak legfeljebb a fele, amint ez a Thales-kör szemléletéből is nyomban adódik.

2. ábra

III. megoldás. A feladat állításán túlmenően bebizonyítjuk, hogy ha

α

hegyesszög, akkor

\begin{matrix} (1 + \frac{1}{sin α}) (1 + \frac{1}{cos α}) \geq 3 + 2 \sqrt[]{2} = 5, 828 ..., \end{matrix}

s hogy egyenlőség csak az

α = 45^{\circ}

esetben következik be. Ennek igazolásához az I. megoldásra hivatkozva elég belátnunk, hogy

\begin{matrix} \frac{1}{sin α} + \frac{1}{cos α} \geq 2 \sqrt[]{2}, \end{matrix}

s hogy itt is csak

α = 45^{\circ}

esetén következik be az egyenlőség. Ezt háromféleképpen bizonyítjuk be.

a)

Az előző megoldás jelöléseit használva

a + b \geq 2 \sqrt[]{2}

a bizonyítandó állitás. Ez abból adódik, hogy

\begin{matrix} {(a + b)}^{2} = (a^{2} + b^{2}) + 2 a b = c^{2} + 2 c m \geq 8. \end{matrix}

Felhasználtuk itt Pythagoras tételét, a terület kétféle kifejezése alapján adódó

a b = c m

összefüggést és az

m = 1

esetben érvényes

c \geq 2

egyenlőtlenséget. Egyenlőség eszerint csak

c = 2 m

esetén, azaz egyenlőszárú derékszögű háromszögre következik be.

b)

Forgassuk el a 2. ábrában a magasságtól balra elhelyezkedő háromszöget felső csúcsa körül pozitív irányban

90^{\circ}

-kal. Így a 3. ábra vastagon megrajzolt részéhez jutunk. A bizonyítandó állítás szerint az

A B

szakasz hosszabb, mint a

45^{\circ}

-kal hajló

A_{1} B_{1}

szakasz, hiszen ennek hossza

2 \sqrt[]{2}

. Azt kell tehát igazolnunk, hogy a derékszögű

A O B ∢

szárait összekötő s a

C

ponton áthaladó szakaszok közül a szimmetrikusan elhelyezkedő

A_{1} B_{1}

szakasz a legrövidebb.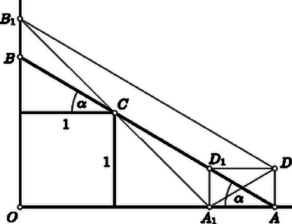

3. ábra

Minthogy az

O A

és

O B

szár között nincs szerepkülönbség, feltehetjük, hogy a

α < 45^{\circ}

. A

B

pont

C

-re vonatkozó tükörképét

D_{1}

-gyel jelöljük. A

C

-re vonatkozó szimmetria miatt a

B B_{1}

A_{1} D_{1}

szakaszok párhuzamosak és egyenlők. A velük párhuzamos és egyenlő

A D

szakasz a

B A D B_{1}

parallelogrammához és az

A_{1} A D D_{1}

téglalaphoz vezet. Az utóbbiból kiolvasható, hogy

A A_{1} D ∢ = A_{1} A D_{1} ∢ = α

, és így

B_{1} A_{1} D ∢ = 135^{\circ} - α > 90^{\circ}

. Eszerint a

B_{1} A_{1} D ▵

-ben

D B_{1}

a legnagyobb oldal, tehát

A_{1} B_{1} < D B_{1} = A B

c)

Felhasználjuk, hogy a pozitív

x

y

számok

a (x, y)

számtani,

g (x, y)

mér-tani és

q (x, y)

négyzetes közepére

\begin{matrix} g (x, y) \leq a (x, y) \leq q (x, y), \end{matrix}

s hogy egyenlőség mindkét esetben csak

x = y

esetén teljesül. Eszerint

\begin{matrix} \frac{1}{sin α} + \frac{1}{cos α} = 2 a (\frac{1}{sin α}, \frac{1}{cos α}) \geq 2 g (\frac{1}{sin α}, \frac{1}{cos α}) = \\ = \frac{2}{g (sin α, cos α)} \geq \frac{2}{q (sin α, cos α)} = 2 \sqrt[]{2} . \end{matrix}

Egyenlőség csak

sin α = cos α

, tehát

α = 45^{\circ}

esetén áll fenn.

Megjegyzés. A feladatban

α

hegyesszöget jelentett. Erre a megszorításra azért volt szükség, mert ha

90^{\circ} < α < 180^{\circ}

vagy

270^{\circ} < α < 360^{\circ}

, akkor a feladat egyenlőtlenségének a baloldalán csak az egyik tényező pozitív, s a szorzat negatív. Ha viszont

180^{\circ} < α < 270^{\circ}

, akkor mindkét tényező negatív, de szorzatuk

1

-nél kisebb. Ennek bizonyítását az olvasóra hagyjuk.