Feladat: 1962. évi Kürschák matematikaverseny 3. feladata Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Kóta József ,  Máté Attila ,  Pósa Lajos ,  Sebestyén Zoltán 
Füzet: 1963/március, 107 - 109. oldal  PDF  |  MathML 
Témakör(ök): Háromszögek nevezetes tételei, Derékszögű háromszögek geometriája, Geometriai egyenlőtlenségek, Ponthalmazok, Kombinatorikus geometria síkban, Tetraéderek, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):Feladatok: 1963/március: 1962. évi Kürschák matematikaverseny 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Feltehetjük, hogy P nincs a DA, DB, DC oldaléleken, mert ha pl. a DA élnek D-től különböző pontja, akkor 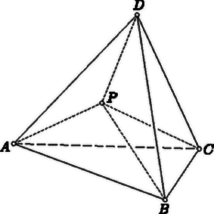PA<DA.
Elég megmutatnunk, hogy az APD, BPD, CPD háromszögek valamelyike P-nél derékszögű vagy tompaszögű. Ha ugyanis pl. az APDΔ ilyen, akkor DA a legnagyobb oldala, s ezért PA<DA (10. ábra).

 
 
10. ábra
 

P-ből induló, PD-vel hegyesszöget bezáró félegyenesek annak a féltérnek a belsejében haladnak, amelyet a P-ben PD-re merőlegesen állított sík határol, s amely tartalmazza a D pontot. Ha tehát az előbb említett háromszögek P-nél mindannyian hegyesszögűek, akkor a gúla minden csúcsa a mondott féltér belsejében van, tehát maga a gúla is, s ez ellentmond annak, hogy P a féltér határsíkján helyezkedik el. Ez az ellentmondás bizonyítja, hogy háromszögeink között valóban van olyan, amely P-nél nem hegyesszögű.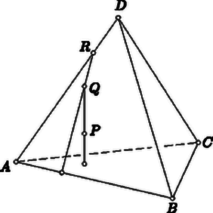
 
 
11. ábra
 

II. megoldás. A P ponton át az ABC síkra merőlegest állítunk. Legyen Q ennek a merőlegesnek az ABC síktól legtávolabbi, még a gúlához tartozó pontja (11. ábra). Q tehát az ABD, ACD, BCD oldallapokon helyezkedik el, legyen pl. az ABD lapon. Állítsunk ennek síkjában a Q ponton át merőlegest az AB egyenesre. Legyen R ennek a merőlegesnek az AB egyenestől legtávolabbi, még az ABD háromszöghöz tartozó pontja. R tehát az AD, BD oldaléleken helyezkedik el, legyen pl. az AD szakasznak pontja.
Ha egy pontot merőlegesen távolítunk egy síktól vagy egy egyenestől, akkor a sík minden pontjától, illetőleg az egyenes minden pontjától távolodik. Ezért
PA≤QA≤RA≤DA.
Mindenütt meg kellett engednünk az egyenlőséget is, hiszen P=Q, Q=R, R=D mindegyike lehetséges. Mindezek azonban egyszerre nem teljesülhetnek, mert P nem azonos D-vel. Ezért legalább egy helyen az egyenlőtlenség jele érvényes, és így PA<DA.
III. megoldás. A PD szakaszt merőlegesen felező sík kettévágja gúlánkat, hiszen P és D a sík más-más oldalán van, és a gúlához tartozik. Ebből következik, hogy e sík által határolt félterek mindegyikének a belsejében van csúcsa a gúlának, mert ha az egyikben nincs, akkor a csúcsaival együtt az egész gúla is a másik féltérben van, s így a sík nem vághatná ketté a gúlát. Ha pl. az A csúcs a P pontot tartalmazó féltér belsejében van, akkor PA<DA, hiszen e féltér belső pontjai közelebb vannak P-hez, mint D-hez.
 
Megjegyzések. 1. Mindhárom megoldásunk a feladat állításán túlmenően azt is bebizonyítja, hogy a PA, PB, PC távolságok között van olyan, amely kisebb, mint a DA, DB, DC távolságok közül a vele azonos végpontú.
2. A második megoldás változtatás nélkül alkalmazható akkor is, ha nem három, hanem akárhány oldalú gúláról van szó. Bizonyítja tehát, hogy egy gúlának a csúcsától különböző (belsejében vagy határán elhelyezkedő) pontja közelebb van az alaplap valamelyik szögpontjához, mint a gúla csúcsa.
3. A harmadik megoldás alapján még többet is kimondhatunk. Módosítás nélkül helyes marad ez a megoldás akkor is, ha benne gúla helyett tetszőleges poliéder szerepel. Bebizonyítja tehát, hogy egy poliéder valamely D csúcsától különböző (belsejében vagy határán elhelyezkedő) pont közelebb van a poliéder valamelyik D-től különböző csúcsához, mint D. Ugyanez az első bizonyítás módszerével is könnyen bizonyítható.
4. Legyenek a háromoldalú gúla oldalélei d1≤d2≤d3, egy a gúla csúcsától különböző pontjának az alapháromszög csúcsaitól mért távolságai pedig p1≤p2≤p3. Az indexezés itt csak a nagyságrendtől függ, és nem jelenti, hogy az azonos indexűeket azonos végpontú szakaszok adják. Kérdezhetjük, hogy ha megadunk valamilyen d1, d2, d3, p1, p2, p3 távolságokat, vajon található-e olyan gúla s abban olyan pont, amelyekhez éppen a megadott értékek tartoznak.
Feladatunk kimondja, hogy
p1<d3
szükséges ahhoz, hogy ez lehetséges legyen. A második megoldásból könnyen kiolvasható, hogy
p1+p2<d2+d3
is szükséges feltétel, hiszen ott PA+PB≤QA+QB≤DA+DB, és az egyenlőség nem teljesülhet mind a két esetben.
Érdemes megemlíteni, hogy pl. p2<d3 már nem kell, hogy teljesüljön, és nem kell teljesülnie a p1+p2+p3<d1+d2+d3 egyenlőtlenségnek sem. Mindez kiolvasható a 12. ábrából, amelyen a szakaszok mellett azok hossza áll. Ezek a tapasztalatok további szükséges feltételek keresésekor óvatosságra intenek.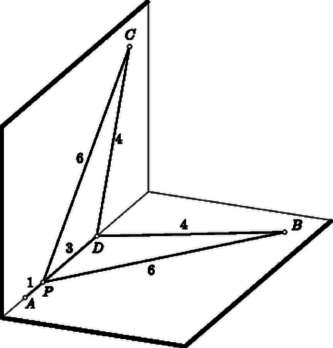
 
 
12. ábra
 

Vannak azonban még további szükséges feltételek is, mert ha a már említettek mind teljesülnek, ez még nem elégséges ahhoz, hogy valóban található legyen a d1, d2, d3, p1, p2, p3 értékeket szolgáltató gúla és pont. Ilyen egyszerű formájú szükséges és elégséges feltétel nem ismeretes. Megkeresése talán érdekes, de nagyon könnyűnek nem látszó feladat.