Kezdőlap


Feladat:	1961. évi Kürschák matematikaverseny 3. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Füzet:	1962/március, 104 - 107. oldal		PDF \| MathML
Témakör(ök):	Körök, Kör geometriája, Deltoidok, Párhuzamos szelők tétele és megfordítása, Tengelyes tükrözés, Vetítések, Egyenlő szárú háromszögek geometriája, Háromszögek hasonlósága, Eltolás, Hatványvonal, hatványpont, Thalesz-kör, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):	Feladatok: 1962/március: 1961. évi Kürschák matematikaverseny 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Az $O_{1}$ , $O_{2}$ középpontú körök $A_{1} A_{2}$ külső és $B_{1} B_{2}$ belső érintőjének metszéspontját $C$ -vel jelöljük (5. ábra). Az $O_{1} A_{1} C B_{1}$ és $C A_{2} O_{2} B_{2}$ derékszögű deltoidok egymáshoz hasonlók, hiszen $C$ -nél elhelyezkedő szögeik mellékszögek, s ebből következik, hogy szögeik páronként egyenlők. Deltoidok körében ez a hasonlóságot valóban biztosítja. A deltoidok $C O_{1}$ , $C O_{2}$ átlói merőlegesek egymásra, mert az említett mellékszögek szögfelezői. Minthogy az $A_{1} B_{1}$ , $A_{2} B_{2}$ átlók mindegyike merőleges a $C O_{1}$ , $C O_{2}$ átlók egyikére (az ugyanazon deltoidbeli átlóra), mindegyikük párhuzamos a másikkal.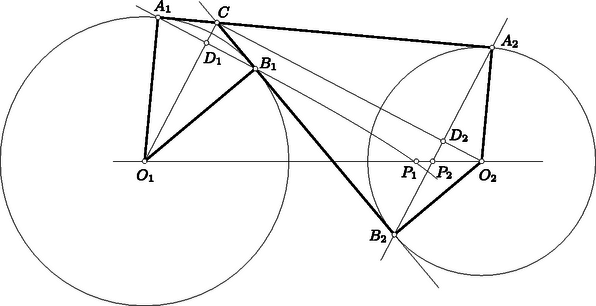
Messék az $A_{1} B_{1}$ , $A_{2} B_{2}$ egyenesek az $O_{1} O_{2}$ centrálist a $P_{1}$ , $P_{2}$ pontokban. Bebizonyítjuk, hogy ez a két pont azonos, hogy tehát az $A_{1} B_{1}$ , $A_{2} B_{2}$ egyenesek metszéspontja valóban a centrálison van. Az 5. ábra szándékosan torz, hogy rajta okoskodásunkat jobban követhessük. Elmondhatjuk, hogy a következőkben ábránk torz voltát bizonyítjuk be.

5. ábra

A deltoidok hasonlóságából következik, hogy átlóik

D_{1}

D_{2}

metszéspontjára

\begin{matrix} O_{1} D_{1} : O_{1} C = C D_{2} : C O_{2} . \end{matrix}

A párhuzamos szelők tétele szerint a

C O_{1} O_{2} ∢

szárait metsző

A_{1} B_{1}

C O_{2}

párhuzamosokra

\begin{matrix} O_{1} D_{1} : O_{1} C = O_{1} P_{1} : O_{1} O_{2}, \end{matrix}

és a

C O_{2} O_{1} ∢

szárait metsző

A_{2} B_{2}

C O_{1}

párhuzamosokra

\begin{matrix} C D_{2} : C O_{2} = O_{1} P_{2} : O_{1} O_{2} . \end{matrix}

Aránypárjaink egybevetéséből következik, hogy

\begin{matrix} O_{1} P_{1} : O_{1} O_{2} = O_{1} P_{2} : O_{1} O_{2}, \end{matrix}

hogy tehát

O_{1} P_{1} = O_{1} P_{2}

, azaz

P_{1}

és

P_{2}

egymással azonos pontok.

II. megoldás. A feladatban előforduló két érintőn kívül a másik

B'_{1} B'_{2}

érintőt is meghúzzuk. Ez az

A_{1} A_{2}

külső érintőt a

D

pontban metszi,

D

-nek a centrálisra vetett vetületét

M

-mel, a centrálisra vonatkozó tükörképét pedig

D'

-vel jelöljük (6. ábra). Bebizonyítjuk, hogy

M

rajta van az

A_{1} B_{1}

A_{2} B_{2}

egyenesek mindegyikén, és ezzel a feladat állítását igazoljuk.
Az

O_{2} D

átmérőjű kör tartalmazza az

A_{2}

B'_{2}

M

pontokat, mert az

O_{2} D

szakasz ezekből a pontokból derékszögben látható. Minthogy

A_{2} O_{2} D ∢ = D O_{2} B_{2}' ∢

, a kerületi szögek tétele szerint

A_{2} M D ∢ = D M B'_{2} ∢

. Ebből a szimmetria révén

A_{2} M D ∢ = D' M B_{2} ∢

következik, tehát az is, hogy az

A_{2}

M

B_{2}

pontok egy egyenesen vannak.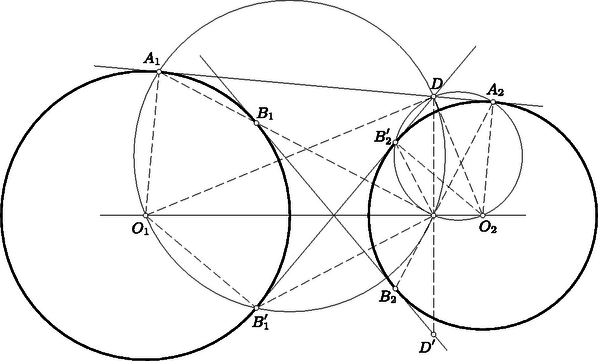

6. ábra

Hasonlóan okoskodhatunk a másik esetben is. Az

O_{1} D

átmérőjű kör tartalmazza az

A_{1}

B'_{1}

M

pontokat, mert az

O_{1} D

szakasz ezekből derékszögben látszik. Minthogy

A_{1} D O ∢ = O_{1} D B'_{1} ∢

, a kerületi szögek tétele szerint

A_{1} M O_{1} ∢ = O_{1} M B'_{1} ∢

. Ebből a szimmetria révén következik, hogy

A_{1} M O_{1} ∢ = B_{1} M O_{1} ∢

, hogy tehát az

A_{1}

B_{1}

M

pontok egy egyenesen vannak.

III. megoldás. Felhasználjuk azt, hogy ha két kör külső és belső érintőjének metszéspontját az egyik érintőn a hozzá legközelebb eső érintési ponttal összekötjük, mindig ugyanakkora szakaszhoz jutunk, bármely érintőpár metszéspontjából indultunk is ki. A 7. ábrán tehát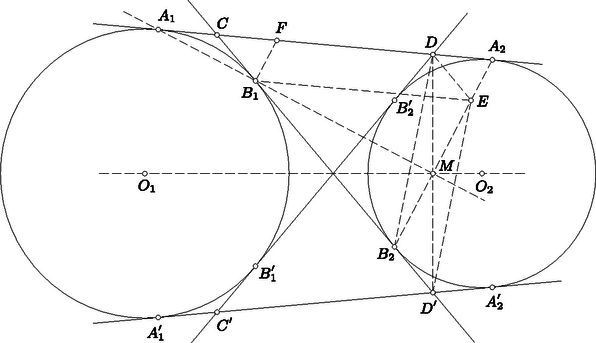

C B_{1} = D A_{2} = D' B_{2}

7. ábra

Abból indulunk ki, hogy az

A_{1} B_{1}

A_{2} B_{2}

egyenesek egymásra merőlegesek. Ezt az első megoldás mintájára láthatjuk be. Az egyenlőszárú

A_{2} B_{2} C ▵

-ből az

A_{2} C

szárral párhuzamos

E B_{1}

szelő egy ugyancsak egyenlőszárú

E B_{2} B_{1} ▵

-et vág le. Ennek alapja az

A_{2} B_{2}

egyenesen, magassága pedig az alapra merőleges

A_{1} B_{1}

egyenesen helyezkedik el. Ezeknek az egyeneseknek az

M

metszéspontja felezi tehát az

E B_{2}

szakaszt.
Az egyenlőszárú

A_{2} B_{2} C ▵

-ből egy az alapjával párhuzamos egyenes az ugyancsak egyenlőszárú

F B_{1} C ▵

-et vágja le. Ennek száraira a megoldás elején mondottak szerint

F C = B_{1} C = A_{2} D

. Ha tehát ezt a háromszöget az

A_{1} A_{2}

egyenes mentén eltoljuk, az

A_{2} E D ▵

-höz jutunk. Ezért

E D

párhuzamos és egyenlő a

B_{1} C

szakasszal, tehát a

D' B_{2}

szakasszal is. Ebből következik, hogy az

E D B_{2} D'

négyszög parallelogramma, hogy tehát

E B_{2}

és

D D'

átlója egymást felezi, azaz

M

felezi a

D D'

szakaszt is. Minthogy a

D

D'

pontok a centrálisra vonatkozólag egymás tükörképei, összekötő szakaszuk

M

felezőpontja a centrálison van. (Ezt a megoldást a versenyen Máté Attila találta, de csak hiányosan dolgozta ki.)
IV. megoldás. A hatványvonalra vonatkozó ismeretekből felhasználjuk azt, hogy mindazok a pontok, amelyekből két egymást metsző körhöz húzott érintőszakaszok egymással egyenlők, a körök közös húrjának az egyenesén vannak.
Ismét abból indulunk ki, amit már az első megoldásban beláttunk, hogy az

A_{1} B_{1}

A_{2} B_{2}

egyenesek egymást az

M

pontban merőlegesen metszik. Thales tétele szerint tehát

M

hozzátartozik az

A_{1} A_{2}

átmérőjű körhöz is a (8. ábra).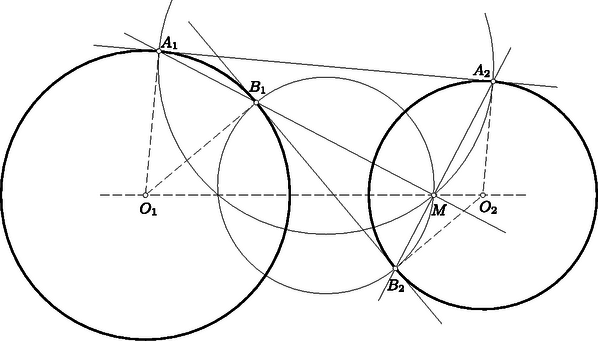

8. ábra

O_{1}

pontból e két körhöz vont érintőkre

O_{1} A_{1} = O_{1} B 1

, s az

O_{2}

pontból hozzájuk vont érintőkre

O_{2} A_{2} = O_{2} B_{2}

. Az előrebocsátottak szerint tehát

O_{1}

és

O_{2}

egy olyan egyenesen van, amely a körök közös

M

pontját tartalmazza. Ez azt bizonyítja, hogy az

O_{1}

O_{2}

M

pontok egy egyenesen vannak.