Kezdőlap


Feladat:	1961. évi Kürschák matematikaverseny 2. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Benczúr András , Bollobás Béla , Fritz József , Kóta Gábor , Kóta József , Molnár Emil
Füzet:	1962/március, 101 - 104. oldal		PDF \| MathML
Témakör(ök):	Másodfokú (és arra visszavezethető) egyenlőtlenségek, Másodfokú függvények, Számsorozatok, Valós számok és tulajdonságaik, Permutációk, Egyenlő szárú háromszögek geometriája, Középvonal, Háromszögek nevezetes tételei, Beírt háromszög, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):	Feladatok: 1962/március: 1961. évi Kürschák matematikaverseny 2. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Abból indulunk ki, hogy ha $0 < a < 1$ , akkor

\begin{matrix} a (1 - a) \leq \frac{1}{4}, \end{matrix}

hiszen ez átrendezéssel keletkezik a nyilván helyes

{(a - \frac{1}{2})}^{2} \geq 0

egyenlőtlenségből. Ebből (és a

b

c

számokra felírt hasonló egyenlőtlenségekből) következik, hogy a feladatunkban szereplő három szorzat szorzata

\begin{matrix} (1 - b) b \cdot (1 - b) c \cdot (1 - c) a = a (1 - a) \cdot b (1 - b) \cdot c (1 - c) \leq {(\frac{1}{4})}^{3} . \end{matrix}

Mind a három vizsgált szorzat tehát nem lehet

\frac{1}{4}

-nél nagyobb, mert akkor a szorzatuk

{(\frac{1}{4})}^{3}

-nél nagyobb volna.

II. megoldás. A vizsgált három szorzat értékhármasa nem változik meg, ha az

a

b

c

számokat ciklikusan felcseréljük (azaz a

b

c

a

vagy a

c

a

b

sorrendre térünk át). Feltehetjük ezért, hogy a három szám közül

a

a legnagyobb, hogy tehát

b \leq a

. Ebből következik, hogy

\begin{matrix} (1 - a) b \leq (1 - a) \leq \frac{1}{4} . \end{matrix}

Az utolsó lépés felhasználta azt az egyenlőtlenséget, amelyből az első megoldás kiindult.

III. megoldás. Egy egységoldalú szabályos

A B C ▵

három csúcsából felmérjük a háromszög más-más oldalára az

a

b

c

távolságokat. A végpontok az

A_{1} B_{1} C_{1} △

-et határozzák meg (3. ábra). Ezt a háromszöget az eredetivé három háromszög egészíti ki. Ezek területe az eredeti háromszög területének rendre

(1 - a) b

(1 - b) c

és

(1 - c) a

-szorosa, hiszen az

A B C △

-ből pl. az

A B

alapot

(1 - a)

-szorosára csökkentve a

C_{1} B C △

-höz, s ennek magasságát

b

-szeresére csökkentve a

C_{1} B A_{1} △

-höz jutunk.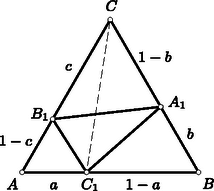

3. ábra

Elég tehát megmutatnunk, hogy ha egy egységterületű szabályos háromszögbe háromszöget írunk, akkor a keletkező három kiegészítő háromszög között van

\frac{1}{4}

-nél nem nagyobb területű. A középvonalak határolta

A_{2} B_{2} C_{2} △

-ről és az ezt kiegészítő háromszögekről tudjuk, hogy területük

\frac{1}{4}

. Állításunk nyilvánvalóan helyes tehát akkor, ha a most említett háromszögek valamelyike tartalmazza beírt

A_{1} B_{1} C_{1} △

-ünk kiegészítő háromszögeinek valamelyikét. Feltehetjük ezért, hogy a középvonalak szétválasztják a rendre a

B C

C A

A B

oldalakon elhelyezkedő

A_{1}

B_{1}

C_{1}

pontokat (4. ábra), mégpedig válassza el a

C_{2} A_{2}

A_{2} B_{2}

B_{2} C_{2}

középvonal rendre az

A_{1}

B_{1}

C_{1}

pontot a másik kettőtől. Ennek az elhelyezkedésnek arra a következményére fogunk támaszkodni, hogy az

A_{1} B_{1}

egyenes metszi az

A B

félegyenest, s hogy a

C_{2} A_{1}

egyenes metszi a

C A

félegyenest. Elegendő most már csak azt bizonyítanunk, hogy az

A_{1} B_{1} C_{1} △

területe

\frac{1}{4}

-nél nagyobb. Ebből következik ugyanis, hogy kiegészítő háromszögeinek területösszege

\frac{3}{4}

-nél kisebb, hogy tehát van közöttük

\frac{1}{4}

-nél kisebb területű.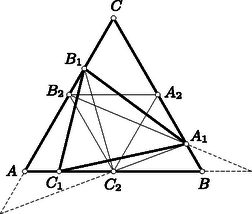

4. ábra

A_{1} B_{1} C_{1} △

területét csökkentjük, ha

C_{1}

csúcsát

C_{2}

-be toljuk el. Ez abból következik, hogy

C_{1}

az eltoláskor közeledik az

A_{1} B_{1}

egyeneshez, hiszen közeledik az

A B

és az

A_{1} B_{1}

egyenesek metszéspontjához. Az

A_{1} B_{1} C_{2} △

területe tovább csökken, ha

B_{1}

csúcsát

B_{2}

-be toljuk el, mert ekkor

B_{1}

A C

C_{1} A_{2}

egyenesek metszéspontjához, tehát az

A_{1} C_{2}

egyeneshez is közeledik. Ha a kapott

A_{1} B_{2} C_{2} △

A

, csúcsát a

B_{2} C_{2}

oldallal párhuzamosan

A_{2}

-be toljuk el, területe nem változik meg. Minthogy területcsökkentéssel az

\frac{1}{4}

területű

A_{2} B_{2} C_{2} △

-höz jutottunk, az

A_{1} B_{1} C_{1} △

területe

\frac{1}{4}

-nél valóban nagyobb.

Megjegyzések. 1. A feladatot megoldó versenyzők nagy többsége az első megoldást találta meg. A második megoldás mondható a legegyszerűbbnek. A harmadik megoldás lényegesen bonyolultabb, viszont rámutat arra a geometriai háttérre, amelyből a feladat származott.

2. Feladatunk az

a

b

c

számokra vonatkozó két megszorítást tartalmaz: megköveteli egyrészt, hogy ezek a számok

1

-nél kisebbek, másrészt azt is, hogy pozitívak legyenek. Egyik megszorításra sincs szükség, de valamelyikre szükség van.
Ha ugyanis csak azt követeljük meg, hogy a számok

1

-nél kisebbek legyenek, akkor

1 - a

1 - b

1 - c

pozitív értékek, s az esetleg előforduló negatív vagy

0

értékű

b

c

a

számmal szorozva

\frac{1}{4}

-nél kisebb szorzatot adnak. Ha viszont csak

a

b

c

pozitivitásához ragaszkodunk, akkor ezeket az esetleg előforduló negatív vagy

0

értékű

1 - c

1 - a

1 - b

értékekkel szorozva jutunk

\frac{1}{4}

-nél kisebb eredményhez. A feladat állítása ezek szerint mindkét esetben csak érdektelen tartalommal bővül. A két bővítés egymástól lényegében nem is különbözik, hiszen a feladat változatlan marad, ha benne

a

b

c

helyébe rendre az

1 - c

1 - b

1 - a

értékeket írjuk. Az

a = \frac{1}{2}

b = 2

c = - 1

példa mutatja, hogy mind a két követelést nem hagyhatjuk el.

3. Első két megoldásunk módszerével (az előző megjegyzésre is támaszkodva) könnyedén bebizonyíthatjuk, hogy ha az

a_{1}, a_{2}, ..., a_{n}

, számok pozitívak, akkor az

\begin{matrix} (1 - a_{1}) a_{2}, (1 - a_{2}) a_{3}, ..., (1 - a_{n}) a_{1} \end{matrix}

szorzatok nem lehetnek mindannyian

\frac{1}{4}

-nél nagyobbak, sőt feladatunk még messzebb menő általánosításaként azt is, hogy ha a pozitív

a_{1}, a_{2}, ..., a_{n}

számoknak egy permutációja

b_{1}, b_{2}, ..., b_{n}

akkor az

\begin{matrix} (1 - a_{1}) b_{1}, (1 - a_{2}) b_{2}, ..., (1 - a_{n}) b_{n} \end{matrix}

számok sem lehetnek mindannyian

\frac{1}{4}

-nél nagyobbak.

4. Feladatunk annak bizonyítását kívánta meg, hogy három szám legkisebbike

\frac{1}{4}

-nél nem nagyobb. Kérdezhetjük, hogy ha ezt a három számot nagyság szerint, rendezzük, mit mondhatunk ki a középsőről és a legnagyobbról. Könnyű belátni, hogy (

0

és

1

közötti számok körében maradva) a középső nem lehet

\frac{1}{2}

-nél nagyobb, s hogy további korlátozása három szám egyikére sem mondható ki.
Ha az előző megjegyzés általánosításainak a körében vetjük fel a hasonló problémát, kérdezve, hogy a nagyság szerint rendezett szorzatok közül az

i

-edikre milyen korlátozásnak kell teljesülnie (

i = 1, 2, ..., n

), akkor már nehezebb problémákhoz jutunk.