Feladat: 1961. évi Kürschák matematikaverseny 1. feladata Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Bollobás Béla ,  Kóta Gábor ,  Kóta József ,  Molnár Emil 
Füzet: 1962/március, 98 - 101. oldal  PDF  |  MathML 
Témakör(ök): Ponthalmazok, Számhalmazok, Geometriai egyenlőtlenségek, Kör geometriája, Négyzetek, Síkbeli szimmetrikus alakzatok, Térbeli szimmetrikus alakzatok, Thalesz-kör, Háromszögek nevezetes tételei, Négyszögek geometriája, Húrnégyszögek, Derékszögű háromszögek geometriája, Egyenlő szárú háromszögek geometriája, Kombinatorikus geometria síkban, Kombinatorikus geometria térben, Tengelyes tükrözés, Síkra vonatkozó tükrözés, Természetes számok, Sík geometriája, Térgeometria, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):Feladatok: 1962/március: 1961. évi Kürschák matematikaverseny 1. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Legyen P1, P2, P3, P4 a sík szóban forgó négy pontja. Válasszuk hosszegységül az általuk meghatározott távolságok legkisebbikét. Azt kell tehát bebizonyítanunk, hogy a hat távolság között van legalább 2 hosszúságú.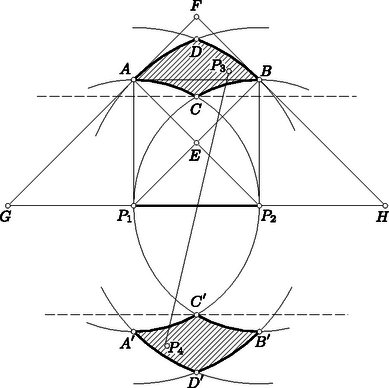
Legyen P1 és P2 egymástól minimális, tehát egységnyi távolságra. Írjunk köréjük egy-egy egységsugarú kört (1. ábra). A P3, P4 pontok egyike sem lehet e körök valamelyikén belül, mert akkor P1P2 nem volna minimális. Írjunk most P1 és P2 köré 2 sugárral egy-egy kört. Ezek a P1P2BA négyzet B, ill. A csúcsán haladnak át. Ha a P3, P4 pontok valamelyike nincs a két most rajzolt kör valamelyikén belül, akkor a kör középpontjától legalább 2 távolságra van.

 

 

1. ábra

 

Ezek szerint csak azzal az esettel kell foglalkoznunk, amikor P3 is és P4 is az utóbb rajzolt körök mindegyikén belül helyezkedik el, de egyikük sincs az előbb rajzolt körök valamelyikének a belsejében. Ez azt jelenti, hogy P3 és P4 ábránk körívekkel határolt, vonalkázott tartományaiban van, de a tartományok határvonalából az AD, DB ívek, valamint az A'D', D'B' ívek pontjait nem számítjuk a tartományokhoz.
Ábránkból kiolvashatjuk, hogy az ACBD ívnégyszög az AB átlójú négyzetben helyezkedik el, s hogy az ívnégyszög pontjai közül csak A és B van a négyzet határvonalán (lásd az alábbi megjegyzést). Ebből a szimmetria miatt mindkét tartományunkra következik, hogy egy tartomány bármely két pontjának távolsága 1-nél kisebb, hiszen egy négyzetben elhelyezkedő szakasz, ha a négyzetnek nem átlója, akkor az átlónál rövidebb. Még nyilvánvalóbb ez a tény, ha arra gondolunk, hogy a négyzet köré írt kör átmérője a négyzet átlója, s hogy a körlemezen elhelyezkedő szakasz, ha nem átmérő, akkor az átmérőnél rövidebb.
Arra az esetre szorítkozhatunk tehát, amikor P3 és P4 más-más vonalkázott tartományhoz tartozik. A C, C' pontokon át párhuzamosokat húzunk a P1P2 szakasszal. E párhuzamosok által határolt sáv elválasztja a két vonalkázott tartományt, és szélessége 2-nél nagyobb, hiszen a CP1 és P1C' egységnyi szakaszok szöge 120∘, azaz nagyobb, mint 90∘. A P3P4 szakasz ezek szerint átvágja az említett sávot, s hossza ezért legalább akkora, mint a sáv szélessége, tehát 2-nél nagyobb.
 
Megjegyzés. Az ábrából olvastuk ki azt, hogy az AB átlójú négyzet tartalmazza az ACBD ívnégyszöget, s hogy az ívnégyszög pontjai közül csak A és B van a négyzet határán. Ezt itt szigorúbban be is bizonyítjuk.
Nyilvánvaló, hogy az A, B pontok az ívnégyszöghöz tartoznak. Elég tehát azt bizonyítanunk, hogy az ívnégyszögnek nincs más pontja a négyzet határán. Nyilvánvaló, hogy az AF, BF egyeneseken nincs az ívnégyszögnek további pontja, hiszen ezek az egyenesek az ívnégyszöget tartalmazó köröket az A, ill. B pontban érintik. Ebből az is következik, hogy ívnégyszögünk az FGH▵-ben helyezkedik el. A P1 középpontú kör AP2, íve kettévágja ezt a háromszöget, és elválasztja az ívnégyszöget az AP2 húrtól. Közös pontjuk csak a húr végpontja lehet. Ezért az ívnégyszögnek nincs az AE szakaszon elhelyezkedő, A-tól különböző pontja. Hasonló indokolással nincs a BE szakaszon elhelyezkedő, B-től különböző pontja sem.
 
II. megoldás. Ha a derékszögű háromszög átfogóját a kisebbik (pontosabban: a másiknál nem nagyobb) befogóval elosztjuk, 2-nél nem kisebb hányadoshoz jutunk. Ez abból következik, hogy a≤b esetén c2=a2+b2≥2a2, tehát c/a≥2.
Ha a háromszög két oldalát változatlanul hagyjuk, de az általuk közrefogott szöget növeljük, akkor a harmadik oldal is növekszik. Ezért tompaszögű háromszögre, sőt (egy egyenesen elhelyezkedő, csatlakozó szakaszokká) elfajuló háromszögre is kimondhatjuk, hogy legnagyobb oldala a legkisebbel osztva legalább 2 értékű hányadost ad.
Elég ezért azt bizonyítanunk, hogy a sík bármely négy pontja között van három olyan, amely derékszögű, tompaszögű vagy elfajuló háromszöget határoz meg. Induljunk ki a sík négy pontjából. Feltehetjük, hogy nincs közöttük három egy egyenesen elhelyezkedő. Tekintsük a négy pont konvex burkát, azaz azt az idomot, amelyet úgy kapunk, hogy a pontok köré fonalat feszítünk. Minthogy a pontok nincsenek mindannyian egy egyenesen, konvex burkuk vagy háromszög, vagy négyszög.
Ha a P1P2P3▵-höz jutunk (2. ábra), akkor P4 ennek belsejében van, hiszen három pont nem lehet egy egyenesen. A P4P1, P4P2, P4P3 szakaszok háromszögünket három háromszögre vágják fel. Ezeknek P4-nél elhelyezkedő három szöge együttesen 360∘, s ezért közöttük tompaszög is van (sőt közülük legalább kettő tompa). Egy ilyen tompaszög a pontjainkból alakított tompaszögű háromszög szöge.
 

 

2. ábra

 

Ha a konvex burok négyszög, akkor ennek a szögeiről elmondhatjuk, hogy nem lehet mindegyik hegyes, hiszen az összegük 360∘. A legnagyobb szög tehát derékszög vagy tompaszög, s ez egy a pontjainkból alakított derékszögű vagy tompaszögű háromszög szöge.
 
Megjegyzések. 1. A feladat állításánál valamivel többet is kimondhatunk. Nemcsak az igaz, hogy a vizsgált hányados nem lehet 2-nél kisebb, hanem az is, hogy 2 a legkisebb olyan szám, amelyre ez igaz. Ezt a négyzet négy csúcsa bizonyítja, hiszen belőlük 2 adódik hányadosul.
Még azzal is kiegészíthetjük a mondottakat, hogy 2 csak egy négyzet csúcsai esetében lép fel hányadosként. Ez mindkét megoldásunkból könnyen kiolvasható.
 
2. Felmerül a kérdés, hogy ha a síknak nem négy, hanem n>2 pontjából indulunk ki, akkor az általuk meghatározott távolságok legnagyobbikát a legkisebbel osztva mekkora hányadoshoz juthatunk. Ez a hányados természetesen tetszőlegesen nagy lehet. Kérdésünk az, hogy mi a hányados lehetséges legkisebb értéke. Azt is kérdezhetjük, hogy a lehetséges legkisebb érték a pontok milyen elhelyezkedése esetén lép fel.
Az n=3 esetben nyilvánvaló, hogy 1 a minimum, s hogy ezt csak a szabályos háromszög csúcsai szolgáltatják. Feladatunk az n=4 esetről szólt. Második megoldásunk módszerével könnyű bebizonyítani, hogy ha n=5, akkor a minimumot a szabályos ötszög csúcsai szolgáltatják, tehát a minimum értéke 12(5+1)≈1,618, s hogy ez más esetben nem lép fel. Ezt a bizonyítást Bollobás Béla a versenydolgozatában el is végezte.
Az n>5 esetekben nem ismeretes a válasz. Megemlítendő mindenesetre, hogy már az n=6 esetben sem adja a szabályos sokszög a minimális értéket, hiszen a szabályos hatszög minden második csúcsát ,,benyomva'' a vizsgált hányados csökken, amit nem nehéz bebizonyítani.
 
3. Még nehezebb a kérdés, ha nem a sík, hanem a tér pontjaira vetjük fel. Itt természetesen csak az n>4 esetekre gondolunk. Már az n=5 eset elintézése sem könnyű. Bizonyítás nélkül megemlítjük, hogy ekkor a minimumot szolgáltató öt pontot úgy kell felvenni, hogy közülük három egy szabályos háromszöget határozzon meg, a másik kettő a háromszög síkjára szimmetrikusan, a háromszög síkjára a háromszög középpontjában emelt merőlegesen helyezkedjék el, és távolságuk a háromszög oldalával legyen egyenlő. A minimum értékére 12/7≈1,309 adódik. Említést érdemel, hogy ez a síkban négy pontra adódó értéknél kisebb.
 
4. A feladatnak még egy másirányú általánosítását is megemlítjük. A sík négy pontjából indulunk ki. Az általuk meghatározott hat távolságot nagyság szerint rendezzük: a legnagyobbal kezdjük, a legkisebbel végezzük, s közben természetesen ismétlődést is megengedünk. Ha e sorozat i-edik elemét a k-adikkal elosztjuk, a q(i,k)-val jelölt hányadoshoz jutunk. Azt kérdezzük, hogy megadott i<k értékekre ez a hányados milyen értékeket vehet fel. Ez a kérdés i és k különféle megválasztásának megfelelően 15 különböző kérdést tartalmaz. Feladatunk csak q(1,6) értékével foglalkozott, és q(1,6)≥2 bizonyítását kívánta. Első megjegyzésünk rámutatott, hogy q(1,6) felveheti a 2 értéket is. Könnyű belátni, hogy minden nagyobb értéket is felvehet. A q(1,6)-ra felvetett kérdésre tehát azt kell felelnünk, hogy q(1,6) értéke lehet minden olyan szám, amely 2-nél nem kisebb.
A többi 14 kérdés vizsgálatát az olvasóra hagyjuk. Különösebb nehézséget egyikük megválaszolása sem jelent, de vigyázni kell, mert a felelet nem minden kérdésre ugyanaz.
Hasonló kérdést vethetünk fel a sík n pontjára, vagy a tér n pontjára is. Így már nehéz kérdésekhez is eljutunk, és csak nagyon kevés rájuk vonatkozó ismert választ említhetnénk. Megemlítjük, hogy a sík 3n pontjára vonatkozólag q(1,3n2+1)≥2. Ezt Turán Pál és Erdős Pál bizonyította be. Bizonyításuk többek között éppen feladatunk állítására támaszkodik. Maga a feladat is innen ered.