Kezdőlap


Feladat:	1960. évi Kürschák matematikaverseny 3. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Bollobás Béla , Máté Attila , Mezei Ferenc
Füzet:	1961/március, 103 - 106. oldal		PDF \| MathML
Témakör(ök):	Hozzáírt körök, Háromszögek nevezetes tételei, Derékszögű háromszögek geometriája, Pitagorasz-tétel alkalmazásai, Paralelogrammák, Rombuszok, Érintőnégyszögek, Szimmetrikus alakzatok, Négyzetek, Háromszögek egybevágósága, Háromszögek hasonlósága, Síkbeli szimmetrikus alakzatok, Kör geometriája, Kúpszeletek, Pont körüli forgatás, Tengelyes tükrözés, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):	Feladatok: 1961/március: 1960. évi Kürschák matematikaverseny 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Ha a $C F G Δ$ -höz írt, az $F G$ oldalt kívülről érintő kör ezt az oldalt $H$ -ban, a $C F$ , $C G$ oldalak meghosszabbítását pedig a $J$ , $K$ pontokban érinti (2. ábra), akkor ez utóbbiakra

\begin{matrix} C J = C K és F J + G K = F G, \end{matrix}

(1)

hiszen az egy pontból ugyanahhoz a körhöz vont érintőszakaszok egyenlők, s ezért

F J = F H

és

G K = G H

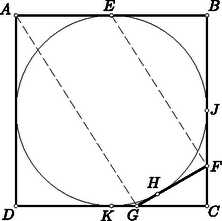2. ábra

Azt állítjuk, hogy

(1)

C F

C G

oldalak meghosszabbításain elhelyezkedő pontpárok közül csak a szóban forgó érintési pontokra teljesül. Ha ugyanis a

J

K

pontokat elmozgatva növeljük vagy csökkentjük a

C J = C K

távolságot, akkor

F J + G K

is növekszik vagy csökken, tehát már nem lehet

F G

-vel egyenlő.
Ezek szerint elég azt bizonyítanunk, hogy a négyzet

B C

C D

oldalainak

J

K

felezőpontjaira

(1)

teljesül, mert ebből következik, hogy a

J

K

pontokban érintő, tehát a négyzetbe írt kör érinti az

F G

oldalt is. Felhasználtuk itt azt, hogy

J

és

K

C F

C G

szakaszok meghosszabbításán van. Ez abból következik, hogy

A C ∥ E J

és

A K ∥ E C

, s ezért a

D G C

sorrendből a

C F J

sorrend, a

B F C

sorrendből pedig a

C G K

sorrend következik.
Legyen a négyzet oldala

2

, azaz válasszuk hosszegységül az oldalhossz felét. Ha tehát

D G = x

, akkor

\begin{matrix} C G = 2 - x, G K = x - 1. \end{matrix}

A D G

F B E

háromszögek hasonlók, mert oldalaik párhuzamosak. Ezért

2 : x = F B : 1

, tehát

F B = 2 / x

, és így

\begin{matrix} C F = 2 - \frac{2}{x}, F J = \frac{2}{x} - 1. \end{matrix}

Minthogy

{(F J + G K)}^{2} = F G^{2}

bizonyítására van szükségünk, Pythagoras tétele szerint már csak

\begin{matrix} {[(\frac{2}{x} - 1) + (x - 1)]}^{2} = {(2 - \frac{2}{x})}^{2} + {(2 - x)}^{2} \end{matrix}

helyességét kell belátnunk. Ez valóban helyes, hiszen a bal oldal

\begin{matrix} {(\frac{2}{x} - 2 + x)}^{2} = {(\frac{2}{x} - 2)}^{2} + 2 x (\frac{2}{x} - 2) + x^{2} \end{matrix}

alakban írható, s itt az utolsó két tag együttes értéke

4 - 4 x + x^{2} = {(2 - x)}^{2}

II. megoldás. Ha a derékszögű

C F G Δ

-höz írt, az

F G

átfogót kívülről érintő kör középpontja

O

(3. ábra), akkor

\begin{matrix} F O G ∢ = 45^{\circ}, \end{matrix}

(2)

hiszen

O F

és

O G

felezi az egymást derékszöggé kiegészítő

J O H

H O K

szögeket, ahol

H

J

K

az előző megoldásban bevezetett pontok.

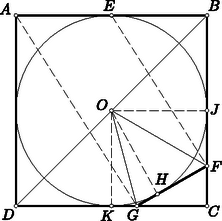3. ábra

Azt állítjuk, hogy

(2)

F C G

derékszög szögfelezőjén elhelyezkedő pontok közül csak a szóban forgó középpontra teljesül. Ha ugyanis

O

a szögfelezőn elmozdulva közeledik a szögfelezőt metsző

F G

szakaszhoz, vagy távolodik tőle, akkor az

F O G

látószög növekszik, illetőleg csökken.
Ezek szerint elég azt bizonyítanunk, hogy

(2)

a négyzet

O

középpontjára teljesül, tehát azt, hogy

\begin{matrix} F O G ∢ = G D O ∢ . \end{matrix}

(3)

E szögek közül az elsőt a

G O D

F O B

szögek, a másodikat a

G O D

O G D

szögek

180^{\circ}

-ra egészítik ki. Ezért

(3)

igazolásához csak

\begin{matrix} F O B ∢ = O G D ∢ \end{matrix}

(4)

bizonyítására van szükség.
Ennek bizonyításához abból indulunk ki, hogy az

A D G

F B E

háromszögek hasonlósága miatt

D G : 2 a = a : B F

, ahol

2 a

a négyzet oldalhossza. Eszerint

D G \cdot B F = 2 a^{2}

, vagyis

D G : D O = B O : B F

, hiszen

D O = B O = a \sqrt[]{2}

. Ebből az aránypárból következik azonban, hogy

G D O Δ \sim O B F Δ

, hiszen ezekben a háromszögekben

G D O ∢ = O B F ∢ = 45^{\circ}

. A hasonlóság miatt a két háromszög megfelelő szögei egyenlők, tehát

(4)

valóban teljesül.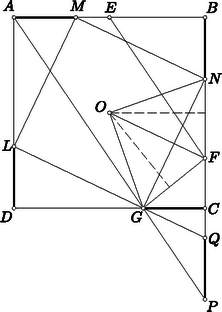

III. megoldás. Mérjük fel négyzetünk négy oldalára a

C G = D L = A M = B N

szakaszokat (4. ábra). A forgásszimmetria miatt

G L M N

is négyzet. Messék az

A G

L G

egyenesek a

B C

egyenest a

P

Q

pontokban. Minthogy az

A L D G

pontnégyes a szerkesztés révén hasonló a

P Q C G

pontnégyeshez, és az előbbiben

A L = D G

, azért a másik pontnégyes megfelelő pontjaira

P Q = C G

. Így tehát

P Q = B N

4. ábra

Minthogy

E F

A P B Δ

középvonala,

F

felezi a

P B

szakaszt, tehát az ezen belül szimmetrikusan elhelyezkedő

Q N

szakaszt is. Eszerint

F

a derékszögű

Q N G Δ

átfogójának felezőpontja, egyenlő távolságra van tehát e háromszög csúcsaitól, azaz

F G = F N

. Ebből következik, hogy

O F G Δ ≃ O F N Δ

, hiszen a forgásszimmetria miatt

O G = O N

, tehát a két háromszög oldalai páronként egyenlők. A bizonyított egybevágóságból következik, hogy az

O

pont az

F G

F N

egyenesektől egyenlő távolságra van, hogy tehát a négyzetbe írt kör az

F G

szakaszt is érinti.

IV. megoldás. Ha az

F

pontot ismerjük, akkor az

A G ∥ E F

előírás egyértelműen meghatározza a

G

pontot. Ha

F

-ből a négyzetbe írt körhöz második érintőt vonunk, akkor ez a

C D

oldalból

F

által ugyancsak egyértelműen meghatározott pontot metsz ki. Feladatunk azt állítja, hogy ez a két hozzárendelés azonos. Ezt most úgy bizonyítjuk, hogy a négyzetbe írt kört érintő

F G

szakaszból indulunk ki, és megmutatjuk, hogy

A G ∥ E F

.
Tekintsük a négyzetbe írt kör mellett a

C F G Δ

-höz írt, a

C F

oldalt kívülről érintő kört (5. ábra). Érintse ez a

C D

egyenest az

R

pontban.

F

a két kör belső hasonlósági pontja, hiszen közös belső érintőik metszéspontja. Ebből következik, hogy a két kört ellentétes oldalról érintő és párhuzamos

A B

D C

egyenesek

E

R

érintési pontjai a hasonlóság által egymáshoz rendelt pontok, hogy tehát az

E

F

R

pontok egy egyenesen vannak.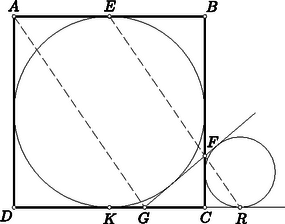

5. ábra

Azt kell bizonyítanunk, hogy

A G

párhuzamos

E F

-fel, azaz

E R

-rel tehát azt, hogy

A E R G

parallelogramma. Ehhez

G R = A E

bizonyítására van szükség. Ez viszont következik abból, hogy egyrészt

A E = K C

, ahol

K

C D

oldal felezőpontja, másrészt pedig

G R = K C

is teljesül, hiszen ismeretes, hogy egy háromszög valamely oldalának két meghosszabbítását a háromszöghöz írt körök az oldalhoz viszonyítva szimmetrikusan elhelyezkedő pontokban érintik.

Megjegyzések. 1. Harmadik feladatunk állítása akkor is helyes, ha benne nem a

B C

C D

oldalakon, hanem a

B C

C D

oldalegyeneseken elhelyezkedő pontokról szólunk, és nem az

F G

szakaszról, hanem az

F G

egyenesről állítjuk, hogy érinti a négyzetbe írt kört. Harmadik megoldásunk közvetlenül alkalmas ennek bizonyítására is, a többinél pedig csekély módosításra van ehhez szükség. Az olvasóra hagyjuk, hogy ezeket a módosításokat megkeresse.
2. Akkor is helyes marad feladatunk állítása, ha nem négyzetről, hanem rombuszról szólunk, és

E

nem az

A B

oldal felezőpontját, hanem a rombuszba írt kör és az

A B

oldal érintési pontját jelenti. Negyedik megoldásunk közvetlenül alkalmazható ennek a bizonyítására is.
A rombuszra kimondott állítás szintén helyes marad, ha a

B C

C D

F G

szakaszok szerepét e szakaszok egyenesei veszik át. A negyedik megoldás az előbb már említett módosítás után ezt is bizonyítja.
3. Pusztán megemlítjük, hogy harmadik feladatunk állítását nagyon gyorsan bizonyíthatja, aki ismeri a kúpszeletek érintőiről szóló Brianchon-tételt, s hogy ez a rövid bizonyítás az előbb említett általánosítások mindegyikét közvetlenül bizonyítja. A részletekbe itt nem bocsátkozhatunk, mert ehhez a középiskolai anyagot messze meghaladó ismeretekre volna szükség.