| Feladat: | 1960. évi Kürschák matematikaverseny 1. feladata | Korcsoport: 18- | Nehézségi fok: nehéz |
| Megoldó(k): | Bollobás Béla , Máté Attila , Mezei Ferenc | ||
| Füzet: | 1961/március, 98 - 100. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Kombinatorikai leszámolási problémák, Logikai feladatok, Gráfelmélet, Természetes számok, Oszthatóság, Kürschák József (korábban Eötvös Loránd) | ||
| Hivatkozás(ok): | Feladatok: 1961/március: 1960. évi Kürschák matematikaverseny 1. feladata | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Megjegyzés. A feladat csak arra az esetre vonatkozik, amikor a társasutazásnak van legalább négy résztvevője. Ha ez nem áll fenn, akkor a feladat feltevése és állítása egyaránt semmitmondó. Az -től különböző, ugyancsak először találkozó utaspárban szerepelnie kell -nak vagy -nek, mert ha ez a utaspár -tól és -től különböző útitársakból állna, akkor , , , közül egyik sem találkozott volna korábban a másik három mindegyikével, és ez ellentmond a feladat feltevésének. Legyen tehát ez az -től különböző, ugyancsak először találkozó utaspár, hiszen minden lehetséges eset ezzé az esetté betűzhető át. Azt vizsgáljuk most, hogy mely -től és -től különböző utaspár állhat olyanokból, akik máskor még nem találkoztak. Az előző bekezdés szerint -nak vagy -nek az ilyen utaspárban is szerepelnie kell, de ugyanolyan indokolással szerepelnie kell benne és valamelyikének is. Eszerint ez a további először találkozó utaspár csak vagy pedig lehet, ahol egy még nem említett résztvevő. Az utóbbi eset azonban lehetetlen, mert akkor az , , , résztvevőkre nem teljesülne a feladat feltevése. Eszerint az , párokon kívül csak állhat egymással először találkozó útitársakból, tehát minden -tól, -től és -től különböző résztvevőnek találkoznia kellett már minden útitársával. Minthogy bármely négy résztvevő között van ilyen, a feladat állítása helyes. Ábrázoljuk a társasutazás résztvevőit egy-egy ponttal, és kössünk össze kettőt-kettőt közülük egy vonaldarabbal akkor, ha a két pontnak megfelelő útitárs korábban még nem találkozott. Az összekötő vonalakat úgy választjuk meg, hogy ne haladjanak át más résztvevőt ábrázoló ponton. Ilyen módon egy gráfhoz jutottunk, amelynek szögpontjai az útitársaknak, élei pedig az először találkozó utaspároknak felelnek meg. Ha a gráf élei esetleg metszik vagy érintik egymást, közös pontjukat nem számítjuk a gráf szögpontjai közé. Az általunk bevezetett gráfnak véges sok szögpontja van, minden éle két-két egymástól különböző szögpontot köt össze, és ugyanazt a szögpontpárt csak legfeljebb egy él köti össze. Ha a következőkben gráfról lesz szó, mindig csak ilyen gráfra gondolunk. Ha feladatunkat a most bevezetett gráfra szövegezzük meg, a feladat a következő alakot ölti: Egy gráfnak nincs négy olyan szögpontja, amelyeknek mindegyikéből kiindul él a másik három szögpont valamelyikéhez. Bebizonyítandó, hogy a gráf bármely négy szögpontja között van olyan, amelyből nem indul ki él. Semmitmondó esetek kizárása kedvéért hozzátehettük volna, hogy a gráfnak legalább négy szögpontja van. Az így szövegezett feladat megoldása rövidebb és áttekinthetőbb. Ezt a közölt megoldás átszövegezésén mutatjuk be: Feltehetjük, hogy a gráfnak van legalább két éle, és , mert különben legfeljebb két szögpont kivételével egyikből sem indul ki él, és bármely négy szögpont között van ilyen. Az , élek egyik végpontja közös, mert különben négy végpontjukra nem teljesülne a feladat feltevése. Ebből az is következik, hogy az , éleken kívül csak olyan él szerepelhet, amelynek van közös pontja -val is és -vel is. Az ilyen él tehát (1. ábra) vagy és szabad végpontját köti össze, vagy pedig közös végpontjukból indul ki. Az utóbbi eset lehetetlen, mert akkor a három él négy végpontja ellentmondana a feladat feltevésének. Ezek szerint csak az , élek három végpontjából indul ki él, bármely négy szögpont között van tehát olyan, amelynek nincs meg ez a tulajdonsága. 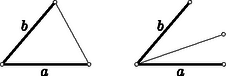 II. megoldás. Feltesszük, hogy van legalább négy olyan résztvevő, aki valamely útitársával a társasutazáson találkozik először, hogy tehát a feladat állítása nem teljesül, és bebizonyítjuk, hogy akkor a feladat feltevése sem teljesülhet, hogy tehát van négy olyan résztvevő, akik közül egyik sem találkozott korábban a másik három mindegyikével. Ez bizonyítja majd, hogy ha a feladat feltevése teljesül, állításának is teljesülnie kell. Ismét abból indulunk ki, hogy és először találkozik egymással. Ha két tőlük különböző résztvevő korábban még nem találkozott, akkor máris találtunk az állításunkat bizonyító négy résztvevőt. Legyen és két olyan további résztvevő, akik nem mindenkivel találkoztak korábban. Mostani feltevésünk szerint biztosan van két ilyen. Az előző bekezdés szerint csak azzal az esettel kell foglalkoznunk, amikor is és is csak már megbetűzött résztvevővel találkozik először. Ekkor azonban , , és négy olyan útitárs, akiknek egyike sem találkozott korábban a másik három mindegyikével, akik tehát állításunk helyességét bizonyítják. Ha ezt a feladatot ugyanúgy átszövegezzük, ahogyan az eredeti feladattal második megoldásunk elején tettük, akkor feladatunk következő újabb szövegéhez jutunk: Egy gráfnak legalább négy szögpontja van, és minden szögpontjából kiindul él. Bebizonyítandó, hogy van a gráfnak négy olyan szögpontja, amelyeknek mindegyikéből kiindul él a másik három valamelyikéhez. Az olvasóra hagyjuk, hogy második megoldásunkat e feladat megoldásává írja át. 2. Második megoldásunk mintájára bebizonyítjuk, hogy utolsó állításunk akkor is helyes, ha benne helyett tetszőleges páros természetes szám áll. Az általánosított feladat tehát a következőképpen szól: Egy gráfnak legalább szögpontja van, és minden szögpontjából kiindul él. Bebizonyítandó, hogy van a gráfnak olyan szögpontja, amelyeknek mindegyikéből kiindul él a többi szögpont valamelyikéhez. Válasszunk ki gráfunkból lehetőleg sok független élt, azaz olyanokat, amelyeknek végpontjai mind különbözők. Ha van független él, akkor ezek végpontjai máris bizonyítják állításunk helyességét. Ha csak független élt választhattunk ki, ha tehát ezektől független -edik él már nincs, akkor végpontjukról tudjuk, hogy minden további szögpontból kiinduló él ennek a végpontnak valamelyikébe fut. Ha tehát ehhez a végponthoz bármely további szögpontot csatolunk, az állításunkat bizonyító szögponthoz jutunk. Megtehetnők, hogy a most bizonyított tényt annyiféleképpen fogalmazzuk át, ahányféleképpen ezt eredeti feladatunkkal megtettük. Megelégszünk azzal, hogy csak az eredeti megszövegezésbe öltöztetett eredményünket mondjuk ki: Ha egy társasutazás bármely résztvevője között van olyan, aki a többi mindegyikével már máskor is találkozott, akkor bármely résztvevő között van olyan, aki már minden útitársával találkozott. Semmitmondó eseteket zárunk ki, ha megköveteljük, hogy a társasutazásnak legalább résztvevője van. Megemlítjük, hogy a esetben az állítás nyilvánvalóan helyes, a eset pedig eredeti feladatunk állítása. 3. Felmerül a kérdés, hogy helyes marad-e utolsó eredményünk, ha benne helyett egy páratlan szám áll. Bebizonyítjuk, hogy így már hamis állításhoz jutunk, hogy tehát ez a módosítás az eddig említett különféle megszövegezések egyikénél sem megengedett. A esetet figyelmen kívül hagyjuk, mert ebben az esetben a feladat értelmét veszti. Bizonyítás céljából elég egy kellően sok független élből álló gráfot tekintenünk. Ennek van legalább szögpontja, és minden szögpontjából kiinduló él. Nincs viszont olyan szögpontja, amelyek mindegyikéből kiindul él a többi szögpont valamelyikébe. Akárhogyan szemelünk ki ugyanis szögpontot, az ezeket összekötő élek végpontjainak száma természetesen csak páros lehet, s így ezek nem meríthetik ki a szögpontot. . |