Feladat: 1959. évi Kürschák matematikaverseny 2. feladata Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Arató Péter ,  Csanak György ,  Halász Gábor ,  Jeltai Árpád ,  Muszély György 
Füzet: 1960/február, 46 - 47. oldal  PDF  |  MathML 
Témakör(ök): Trigonometriai azonosságok, Trigonometrikus függvények, Paralelogrammák, Egyenlő szárú háromszögek geometriája, Húrnégyszögek, Thalesz-kör, Derékszögű háromszögek geometriája, Pitagorasz-tétel alkalmazásai, Beírt kör középpontja, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):Feladatok: 1960/február: 1959. évi Kürschák matematikaverseny 2. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Igen egyszerű trigonometriai megoldás kínálkozik a feladatra és a versenyzők mind ilyen utat is választottak.

 

I. megoldás. Jelöljük a torony magasságát méterben mérve x-szel, a látószögét 100, 200, 300m-ről rendre α, β, γ-val, ekkor
tgα=x100,tgβ=x200,tgγ=x300,
és feltétel szerint α+β+γ=90∘, tehát
tgγ=x300=tg[90∘-(α+β)]=ctg(α+β)=ctgαctgβ-1ctgα+ctgβ==100x⋅200x-1100x+200x=100⋅200-x2300x.


Innen
2x2=100⋅200,
és mivel x gyanánt csak pozitív érték jön számításba, tehát a torony magassága x=100m.
Megjegyzés. Mint többen észrevették, megoldható a feladat ugyanezzel a gondolatmenettel akkor is, ha tetszés szerinti a, b, c távolságokból mért α, β, γ látószögekről tudjuk azt, hogy összegük 90∘. Ekkor a torony magassága abc/(a+b+c).
Megoldható azonban a feladat lényegesen egyszerűbb összefüggésekre támaszkodva is.
 

II. megoldás. Sík talajon nem lényeges, hogy milyen irányból mérjük a torony látószögét az adott távolságokból, válasszuk tehát a 100, ill. 200m távolságra levő A, ill. B pontokat a toronytól egymással ellentétes irányban, a γ látószöget pedig szemléltessük úgy, hogy a B pontból az AB egyenesnek a torony C csúcsával ellentétes oldalán mérünk fel AB-re merőlegesen a torony magasságával egyenlő BD távolságot. Ekkor 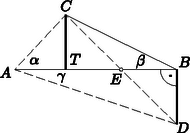BAD∢=γ, mert AB=300m.
 
 

1. ábra
 

A torony T talppontja, C csúcsa továbbá a B és D pontok meghatározta négyszög paralelogramma, mert két oldala egymással párhuzamos és egyenlő, tehát CD a TB szakaszt E felezőpontjában metszi. Eszerint ET=100m, s így TEC∢=α, az ACE háromszög egyenlő szárú. Megállapíthatjuk C-nél levő szögének a nagyságát is abból, hogy az ADBC négyszög A-nál és B-nél levő (szemben fekvő) szögeinek összege α+γ+β+90∘, a feltétel szerint 180∘-ot ad; a négyszög tehát húrnégyszög, és AD a körülírt kör átmérője, mert a B pontból 90∘-os szögben látszik. Így az ACD∢=ACE∢ szintén 90∘-os, az ACE egyenlő szárú háromszög tehát derékszögű. Ebből adódik, hogy α=45∘, így az ATC derékszögű háromszög ugyancsak egyenlő szárú, tehát a torony magassága 100m.
 

III. megoldás. Rajzoljuk meg a tornyot háromféleképpen. Két oldalról egyrészt az α és β látószögű egyenesekkel, másrészt β és γ, harmadrészt γ és α látószögű egyenesekkel (2. ábra). A keletkező három háromszögben az A1B1, B2C2, C3A3 oldalakon levő szögek összege 2α+2β+2γ=180∘, így a D1, D2, D3-nál levő szögek összege 360∘. Mivel még B1D1=B2D2, C2D2=C3D3, A3D3=A1D1, így a három háromszög egy ABC háromszöggé tehető össze. Ennek oldalai AB=300m, BC=500m, CA=400m kielégítik a
BC2=CA2+AB2
összefüggést, és ismeretes, hogy ebből következik a háromszög derékszögű volta, (a Pythagorász-tétel megfordítható) derékszöggel az A csúcsnál. Így 2α=90∘, és ebből következik, hogy a torony 100m magas.
 
 

2. ábra
 

Megjegyzés. A II. megoldás lényegesen kihasználja a feladat speciális adatait, a III. azonban csak részben. Ha ugyanis megfigyeljük, hogy az összeillesztésnél a D1, D2, D3 egybeesésével keletkező D pont az ABC háromszög beírt körének a középpontja, akkor területszámítás segítségével más távolságadatok mellett is meghatározható a torony magassága.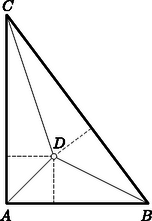
 
 

3. ábra