Feladat: 1958. évi Kürschák matematikaverseny 1. feladata Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Bollobás Béla ,  Győhy Kálmán ,  Kisvölcsey Jenő ,  Montvay István ,  Sárközy András ,  Tihanyi Ambrus 
Füzet: 1959/március, 67 - 69. oldal  PDF  |  MathML 
Témakör(ök): Sík geometriája, Háromszögek nevezetes tételei, Ponthalmazok, Négyszögek geometriája, Egyéb sokszögek geometriája, Szabályos sokszögek geometriája, Pont körüli forgatás, Kombinatorikus geometria síkban, Természetes számok, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):Feladatok: 1959/március: 1958. évi Kürschák matematikaverseny 1. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A feladat állítása a következővel egyértelmű: van olyan 3 pont, amelyek valamelyikéből a másik kettőn át húzott félegyenesek hajlásszöge legalább 120∘-os. Ebben a formában fogjuk bizonyítani az állítást.

 
I. megoldás. A következő segédtételből indulunk ki. Ha egy háromszög belsejében adva van egy P pont, akkor a P-ből a csúcsokhoz húzott egyenesek hajlásszögének valamelyike legalább 120∘-os. Valóban, véve a három szög legnagyobbikát (illetőleg az ilyenek egyikét), ennek a háromszorosa legalább akkora, mint a három szög összege, vagyis legalább 360∘, ez a szög tehát legalább 120∘-os.
Ebből következik, hogy a feladat állítása teljesül minden olyan esetben, amelyben kiválaszthatók az adott pontok közül egy háromszög csúcsai úgy, hogy ez a háromszög tartalmazzon adott pontot.
 
 

1. ábra
 

Válasszunk ki most már az adott 6 pont közül hármat. Ha abban a háromszögben amelynek ezek a csúcsai, van még adott pont, akkor, mint láttuk, teljesül a feladat állítása; de teljesül akkor is, ha a háromszög két oldalának a közös csúcsukon túli meghosszabbításai közt levő szögtartományba esik adott pont (1. ábra), mert akkor a kérdéses csúcsot tartalmazza az a háromszög, amelyet a másik két csúcs és a negyedik pont határoz meg. A síkot a háromszög oldalegyeneseivel felosztva feltehetjük tehát, hogy a további adott pontok a háromszög oldalaihoz csatlakozó síkrészekben helyezkednek el. Hozzávéve közülük egyet a már kiválasztottakhoz, a tekintetbe vett pontok egy konvex négyszög csúcsai (2. ábra).
 
 

2. ábra
 

Meghúzva a négyszög még hiányzó két oldalának egyenesét, ismét feltehetjük, hogy sem a keletkező új háromszögbe, sem pedig az oldalmeghosszabbítások közti szögtartományokba nem esik adott pont. Így véve egy ötödik pontot az az előzőkkel konvex ötszöget alkot, és a gondolatmenetet még egyszer megismételve nyerjük, hogy elég azt az esetet megvizsgálni, amelyben az adott pontok egy konvex hatszög csúcsai. Ebben az esetben a hatszög legnagyobb szögének, vagy a legnagyobbak egyikének a hatszorosa legalább akkora, mint a hat szög összege, tehát legalább 720∘, s így a szög legalább 120∘-os. Ezzel igazoltuk a feladat állítását.
 
II. megoldás. Az adott pontok vagy egy konvex hatszög csúcsai, vagy közülük 3, 4 vagy 5 egy olyan konvex sokszög csúcsait alkotja, amely tartalmazza a többi adott pontot. Az így kapott hat‐, ill. három‐, négy‐ vagy ötszöget az adott pontok konvex burkának nevezzük.1
Ha a konvex burok hatszög, akkor, mint az előző megoldás végén láttuk, egyik szöge legalább 120∘-os.
Ha a konvex burok négy‐, vagy ötszög, akkor egyik átlójával, ill. egyik csúcsából induló átlóival háromszögekre bontjuk. A keletkező háromszögek valamelyike tartalmaz adott pontot. A hátralevő esetek mindegyikében találunk tehát olyan háromszöget, amelynek a csúcsai adott pontok és amely tartalmaz ezeken kívül is adott pontot. Az előző megoldás elején láttuk, hogy ekkor a csúcsokat a további adott ponttal összekötő szakaszok közti szögek valamelyike legalább 120∘-os. Ezzel igazoltuk a feladat állítását.
 
Megjegyzések. a) Nem lényeges annak kikötése, hogy semelyik 3 pont sincs egy egyenesen, ha ugyanis 3 pont egy egyenesen van, akkor a középsőből a két szélsőhöz húzott félegyenesek 180∘-os (tehát 120∘-nál nagyobb) szöget zárnak be.
b) Vizsgáljuk meg, előfordulhat-e, hogy az adott pontok mindegyikét minden lehető módon összekötve két-két másikkal, a keletkező forgásszögek legnagyobbika sem nagyobb 120∘-nál, és ha igen, milyen esetekben következik ez be. A bizonyításból azonnal adódik, hogyha a 6 pont konvex burka hatszög, akkor a kérdéses legnagyobb szög akkor 120∘-os, ha a hatszög minden szöge egyenlő, vagyis, ha az oldalai rendre párhuzamosak egy szabályos hatszög oldalaival (nem kell azonban szabályosnak lennie a hatszögnek, mint azt több versenyző állította).
Ha az adott pontok konvex burka nem hatszög, akkor láttuk, hogy kiválaszthatók a pontok közül egy olyan háromszög csúcsai, amely tartalmaz legalább még egy adott P pontot. A bízonyításból világos az is, hogy P-ből a háromszög oldalainak 120∘-os szögben kell látszaniuk, mert különben valamelyik biztosan 120∘-nál nagyobb szög alatt látszik.
 
 

3. ábra
 

Ha teljesül is ez a feltétel, akkor is fellép 120∘-nál nagyobb szög, amint legalább még egy Q pont van adva (3. ábra). Ha ugyanis Q a P-ből a csúcsokhoz mutató félegyenesek valamelyikén van, akkor arra 3 pont esik, és így van 180∘-os szög is. Ha pedig Q az említett félegyenesek közti 120∘-os szögtartományok belsejében van, akkor a P-ből Q-n át húzott félegyenes a szögtéren kívül levő félegyenessel 120∘-nál nagyobb szöget zár be. Ezzel bebizonyítottuk a következőt: hat adott pont mindegyikéből minden két-két ponthoz húzott félegyenes-párok közötti szögek legnagyobbika legalább akkora, mint a szabályos hatszög egy szöge, és csak abban az esetben pontosan akkora, ha az adott pontok egy olyan konvex hatszög csúcsai, amelynek az oldalai párhuzamosak egy szabályos hatszög oldalaival.
c) A most kimondott állítás 6 helyett 3, 4 vagy 5 pont esetére is igaz. Ha ugyanis mindegyik pont csúcsa a pontrendszer konvex burkának, akkor a sokszög legnagyobb szöge legalább akkora, mint a szabályos három‐, négy‐, ill. ötszög egy szöge, és pontosan ekkora csak úgy lehet, ha a sokszög minden szöge ekkora, vagyis ha oldalai párhuzamosak egy ugyanennyi oldalú szabályos sokszög oldalaival. Ha pedig (4 vagy 5 adott pont esetén) van olyan pont, amelyik nem csúcsa a konvex buroknak, akkor egy ilyen pont körül, mint már láttuk, fellép legalább 120∘-os szög, viszont a szabályos négy‐ és ötszög egy szöge kisebb 120∘-nál.
Megmutatjuk, hogy a most belátott szabályosság 7 adott pont esetén már nem áll fenn: a síkban 7 pont közül valamelyiket össze tudjuk kötni két másikkal úgy, hogy 120∘-nál nagyobb szög keletkezzék, viszont bárhogy adunk meg egy 120∘-nál nagyobb szöget, mindig megadható 7 pont úgy, hogy a köztük fellépő összes szögek kisebbek legyenek az adott szögnél. Hozzátesszük, hogy az utoljára említett pontrendszerek már nem lesznek általában konvex 7-szög csucsai.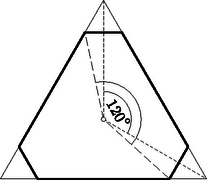
 
 

4. ábra
 

Ha a 7 pont konvex burka 7-nél kevesebb oldalú, akkor az állítás első része következik a b) pontban bizonyított állításból. Ha pedig az adott pontok egy konvex 7-szög csúcsai, akkor ennek legnagyobb szöge legalább akkora, mint a szabályos 7-szög egy szöge, ez pedig nagyobb mint 120∘. Az állítás második felének igazolására vágjuk le egy szabályos háromszög csúcsait a csúcsokhoz közel a szemközti oldallal párhuzamos egyenessel, és az így keletkező hatszög csúcsaihoz vegyük hozzá a háromszög középpontját (4. ábra). Ekkor könnyen beláthatjuk, hegy a fellépő legnagyobb szög is tetszés szerint közel lesz 120∘-hoz.
d) Az elmondott eredmények L. M. Blumenthal amerikai matematikustól származnak.2 Ő vetette fel általában a kérdést, hogy milyen alsó korlátot lehet megadni tetszés szerinti n pont esetén a fellépő legnagyobb szögre. Szekeres György megmutatta,3 hogy ha a pontok egy síkban vannak és számuk 2k (k természetes szám), akkor az (1-1k)180∘-os szög játszik hasonló szerepet, mint 7 pont esetén a 120∘, és térben is nyert hasonló eredményeket. Még síkban sincs azonban minden n-re megoldva a probléma.
1Képzeljünk a pontokban a síkra merőlegesen gombostűket betűzve és vegyük körül ezeket cérnával, majd húzzuk össze a cérnát a legrövidebbre, ekkor a cérna megadja a konvex burkot.

2Journal of the American Mathematical Society, 61, (1939), 912‐922. o.

3Ugyanott, 63, (1941), 208‐210. o.