| Feladat: | 1957. évi Kürschák matematikaverseny 1. feladata | Korcsoport: 18- | Nehézségi fok: nehéz |
| Megoldó(k): | Makkai Mihály , Szebeni András , Verhás József | ||
| Füzet: | 1958/február, 38 - 40. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Részhalmazok, Gráfelmélet, Hamilton-út, -kör, Egyéb szinezési problémák, Kombinatorikai leszámolási problémák, Kürschák József (korábban Eötvös Loránd) | ||
| Hivatkozás(ok): | Feladatok: 1958/január: 1957. évi Kürschák matematikaverseny 1. feladata | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Az síkjának pontjában a síkra merőleges egyenest állítunk, és ezen az egyenesen egy pontot veszünk fel. Vizsgáljuk, mitől függ az, hogy megválasztható-e a feladat kívánalmának megfelelően, úgy tehát, hogy az , , háromszögek mindegyike hegyesszögű legyen. Most az , , háromszögek csúcsú szögeit vizsgáljuk. Tudjuk, hogy a síkban egy pontból egy szakasz akkor látható hegyes szögben, ha a pont a szakasz Thales-körén kívül van. A három vizsgált szög tehát akkor hegyes szög, ha messzebb van az három oldalának felezőpontjától, mint e három oldal hosszának fele. Ilyen pont mindig van a -ben emelt merőleges egyenesen, bárhogyan választjuk is meg a pontot, hiszen elég pl. azt megkövetelni, hogy messzebb legyen az síktól, mint az oldalai leghosszabbikának a fele. Az elmondottakból következik, hogy a feladat kérdésére felelünk, ha azoknak a pontoknak a mértani helyét állapítjuk meg, amelyekre a fentebb felsorolt hat szög mindegyike hegyes. A és mindegyike akkor és csak akkor hegyes, ha annak a síksávnak belsejében van, amelyet az , pontokban -re emelt merőlegesek határolnak. Ez abból következik, hogy pl. a akkor hegyes, ha az -ban emelt merőlegesnek ugyanazon az oldalán van, mint a pont. A keresett mértani hely ezek szerint három síksáv belsejének közös részeként adódik, s e síksávokat az oldalaira végpontjaikban emelt merőlegesek határolják. Ha hegyesszögű -ből indulunk ki, akkor a három sáv közös részeként hatszög adódik (lásd 1. ábra), s a keresett mértani hely e hatszög belseje. 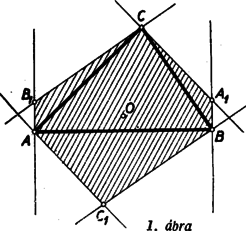 Megjegyzések. 1. Ha az nem hegyesszögű, akkor a szerepeltetett síksávok közös része nem hatszög, hanem parallelogramma, és e parallelogramma belseje adja a vizsgált mértani helyet. A 2. ábra derékszögű és tompaszögű háromszög esetében mutatja be ezt a mértani helyet. 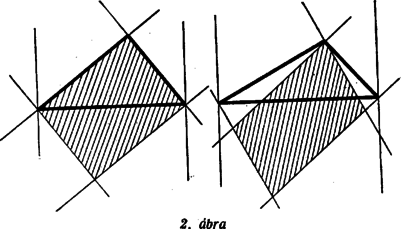 2. Hegyesszögű háromszög esetében akkor is beláthatjuk, hogy mértani helyként valóban hatszög adódik, ha az ábra szemléletére nem támaszkodunk. Evégből először azt állapítjuk meg, hogy a szereplő síksávok mindegyike szimmetrikus a háromszög köré írt kör középpontjára vonatkozólag, hiszen ez a pont a sávok középvonalain, az oldalak felező merőlegesein helyezkedik el. Ebből következik, hogy a három sáv közös része is szimmetrikus ugyanerre a pontra vonatkozólag. A és szélességű sávok közös része egy csúcsú parallelogramma, hiszen ez a két sáv nem párhuzamos egymással. Minthogy az hegyesszögű, a harmadik, szélességű sáv belsejében van, és ezért a három sáv közös részének is csúcsa. Hasonló indokolással ugyanezt az és pontokról is elmondhatjuk. Az -ra vonatkozó centrális szimmetriából következik tehát, hogy az , , pontoknak -ra vonatkozó tükörképei, az , , pontok, ugyancsak szerepelnek a közös rész csúcsai között. Az , , , , , pontok mind különbözők, mert nem azonos az oldalai egyikének felezőpontjával, valamint egyik csúcsával sem. Több csúcsa a közös részként adódó sokszögnek nem lehet, mert a három sávnak együttesen hat határegyenese van, és ezért a közös résznek hatnál több oldala nem lehet. A közös rész ezek szerint valóban hatszög. 3. Az , , pontokhoz nemcsak úgy juthatunk el, hogy az , , pontokat az pontra vonatkozólag tükrözzük, hanem úgy is, hogy az magasságpontját tükrözzük az oldalak felezőpontjaira vonatkozólag. (3. ábra) 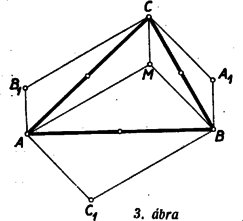 Ez abból következik, hogy ha jelöli a pontnak az oldal felezőpontjára vonatkozó tükörképét, akkor parallelogramma. Ezért és is merőlegesek a , ill. oldalakra, tehát két magasságvonal metszéspontja, azaz a magasságponttal azonos. A most belátott tényből következik, hogy hatszögünk területe az területének kétszerese, hiszen e háromszögön túlnyúló részei egybevágók az , , háromszögekkel, és ezek együttesen az -et alkotják. 4. A feladat megoldása módot nyújt 4 olyan pont meghatározására, amelyek közül akárhogyan választunk is ki hármat, mindig egy hegyesszögű háromszög három csúcsához jutunk. Megemlítjük, hogy senkinek sem sikerült eddig feleletet adni arra a kérdésre, vajon 4 helyett legfeljebb hány ilyen tulajdonságú pontot lehet megadni. |