| Feladat: | 1954. évi Kürschák matematikaverseny 3. feladata | Korcsoport: 18- | Nehézségi fok: nehéz |
| Megoldó(k): | Balatoni Ferenc , Bárdos András , Csiszár Imre , Kovács László , Vigassy József | ||
| Füzet: | 1955/április, 103 - 105. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Természetes számok, Kombinatorikai leszámolási problémák, Részhalmazok, Szabályos sokszögek geometriája, Irányított gráfok, Teljes indukció módszere, Kürschák József (korábban Eötvös Loránd) | ||
| Hivatkozás(ok): | Feladatok: 1955/január: 1954. évi Kürschák matematikaverseny 3. feladata | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. megoldás. Legyen olyan résztvevő, akinél több győzelmet senki sem aratott. Ha nem felelne meg a feladat követelményének, akkor volna olyan versenyző, akit sem , sem az által legyőzöttek nem győztek le, aki tehát mindezeket megverte, s így legalább eggyel több győzelmet aratott, mint . Ez azonban lehetetlenség, mert -nál több győzelmet senki sem aratott, ezért megfelel a feladat követelményének. II. megoldás. Legyen a versenyzők egyike. Ha az által a feladat előírása szerint végzett felsorolásban nem szerepel minden más versenyző, akkor jelöljük az általa nem említett versenyzők összességét -gyel. Minthogy ezeket nem említette, mindegyikük megverte -et és az által legyőzötteket. Ezért a csoport minden tagja megemlíti az által említetteket, ha az előírt felsorolást elvégzi. Legyen egy tagja a csoportnak. Ha felsorolásában nem szerepel minden más versenyző, akkor tehát a nem említettek mind -be tartoznak, s ezek összességét -vel jelöljük. Mivel ezeket nem említette, mindegyikük megverte -t és az által legyőzötteket, ezért a csoport minden tagja megemlíti felsorolásában az által említetteket. Így tovább haladva egyre kevesebb versenyzőből álló , , csoportokhoz jutunk, amíg el nem érünk olyan versenyzőhöz, akinek felsorolásában minden versenytársa szerepel. Minthogy a csökkenő csoportok sorozata nem lehet végtelen, el kell hogy jussunk ilyen versenyzőhöz. Megjegyzés: A közölt megoldás burkoltan teljes indukcióra épül. Okoskodását a következőképpen is előadhatjuk: Ha csak két résztvevő van, a feladat állítása helyes; tegyük fel, hogy az állítás helyes, ha a résztvevők száma -nél kevesebb; az versenyző közül kiválasztott versenyző egy csoportot határoz meg, hacsak maga meg nem felel a követelménynek; -ben -nél kevesebb résztvevő van, az indukciós feltevés szerint van tehát közöttük olyan, akinek felsorolásában -nek minden más tagja szerepel, a fentebbiek szerint viszont a -be nem tartozók mindegyikét is említi, ez a versenyző tehát megfelel a feladat követelményének. III. megoldás. Az állítást teljes indukcióval bizonyítjuk. Ha csak két résztvevő van, az állítás nyilván helyes. Tegyük fel, hogy helyes az állítás, ha résztvevő van. Ha tehát résztvevő van, akkor van az első között olyan résztvevő, akinek felsorolásában minden más versenyző szerepel az első közül. Legyen az -edik résztvevő. Ha is szerepel felsorolásában, akkor megfelel a követelménynek. Ha nem szerepel felsorolásában, akkor le kellett hogy győzze -t és azokat, akiket legyőzött; ezért -nek felsorolásában szerepel és mindazok, akiket felsorolt; ekkor tehát megfelel a követelménynek. IV. megoldás. A versenyzők egy teremben helyezkednek el. Az egyik versenyző kivezeti a teremből azokat, akiket legyőzött (esetleg senkit sem). Ha van még, aki a teremben marad, egyikük újból kivezeti azokat, akiket legyőzött a teremben maradottak közül. Ezt folytatják mindaddig, amíg valaki a termet ki nem üríti. A kiürítő legyőzte azokat, akiket kivezet, és azokat, akik korábban kivezettek, hiszen a teremben maradhatott, ez utóbbiak viszont legyőzték az általuk kivezetetteket. A kiürítő tehát minden társát megemlíti felsorolásában. Megjegyzések: 1. Az első megoldás mutatja, hogy a győztes (vagy a győztesek bármelyike) megfelel a követelménynek. Nem igaz azonban, hogy csak győztes felelhet meg. Sőt még a vesztes is megfelelhet, ezt az alábbi eredménytáblázat példája bizonyítja: 2. Az is lehetséges, hogy a verseny minden résztvevője megfelel a feladat követelményének. A fenti eredménytáblázat erre is példát nyújt. Mutatja, hogy 5 versenyző esetében ez is lehetséges. Felvetjük a kérdést, hogy hány résztvevős versenyben lehetséges ez. Ha két résztvevő van, nyilvánvaló, hogy csak egyikük (a győztes) felel meg a követelménynek. Négy résztvevős versenyben sem felelhetnek meg mind a négyen a feladat követelményének. Ha ugyanis van közöttük olyan résztvevő, aki három győzelmet aratott, akkor a többinek felsorolásában ez a versenyző nem szerepel. Ha van olyan résztvevő, akit mindenki legyőzött, akkor ennek felsorolásában senki sem szerepel. Ha viszont mindannyian egy vagy két győzelmet arattak, akkor ketten egyszer-egyszer, ketten pedig kétszer-kétszer győztek, hiszen összesen hat mérkőzés volt; a két egygyőzelmes versenyző egyike legyőzte a másikat, az elsőnek felsorolásában tehát csak két versenytársa (a másik és akit az legyőzött) szerepel. Bizonyítjuk, hogy ha a résztvevők száma nem Ezt először arra az esetre bizonyítjuk, amikor a versenyzők száma, Ha a versenyzők száma páros és 4-nél több, legyen közöttük A 7. ábra bemutatja az előírásunk szerinti versenyeredményeket 5 és 6 résztvevő esetében. 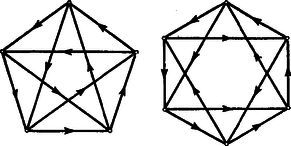 Az ábrán a nyíl a győztestől a vesztes felé irányul. A 6 versenyzős esetben az átellenesen állók mérkőzéseinek (elő sem írt) eredményét ábránk nem is jelzi. |