| Feladat: | 1954. évi Kürschák matematikaverseny 2. feladata | Korcsoport: 18- | Nehézségi fok: nehéz |
| Megoldó(k): | Balatoni Ferenc , Bárdos András , Csiszár Imre , Kovács László , Vigassy József | ||
| Füzet: | 1955/április, 101 - 103. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Gömbi geometria, Gömb és részei, Térelemek és részeik, Húrnégyszögek, Kör geometriája, Sokszögek szimmetriái, Trapézok, Tengely körüli forgatás, Kürschák József (korábban Eötvös Loránd) | ||
| Hivatkozás(ok): | Feladatok: 1955/január: 1954. évi Kürschák matematikaverseny 2. feladata | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Megjegyzések: 1. Legrövidebben a következő módon indokolhatjuk az állítás helyességét: Tekintsük a testnek egy leghosszabb húrját. E húron átfektetett sík körben metsz, s a húr ennek a körnek átmérője, hiszen különben ennek a körnek, tehát magának a testnek is volna a kiszemeltnél hosszabb húrja. Ebből azonban az következik, hogy a test azonos avval a gömbbel, melynek egyik átmérője a kiszemelt húr. ‐ Ez az okoskodás hiányos, mert nem bizonyítja, hogy van leghosszabb húr. Okoskodásunk bizonyítássá válnék, ha ezt is bizonyítanók, ehhez azonban a felsőbb matematika eszközeinek használatára volna szükség.  E négy pont által meghatározott trapéz húrnégyszög, hiszen síkja a testet körben metszi; ezért e trapéz szimmetrikus (szemközti szögei kiegészítő szögek, ezért egy párhuzamos oldalon egyenlő szögek nyugszanak). Szimmetrikus trapéznál a párhuzamos oldalak felezőpontjait összekötő egyenes merőleges a párhuzamos oldalakra, így tehát a körközéppontokat összekötő egyenes merőleges a körök síkjaira. Ezek szerint, ha a két sík egyikét párhuzamosan eltoljuk, az adódó körmetszet középpontja mindig rajt van a másik kör középpontjában síkjára emelt merőlegesen. Ez az egyenes tehát forgástengelye testünknek, testünk forgástest. A forgástengelyen átfektetett sík is körben metszi azonban a testet, és a szimmetria miatt e kör középpontja a forgástengelyen van. A szereplő forgástest tehát gömb. II. megoldás. Tekintsük a testnek egy középpontú körmetszetét (5. ábra). 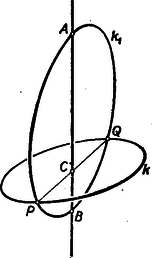 Ennek síkjára pontban merőlegest állítunk. Fektessünk át egy síkot e merőlegesen. Ez a sík a kört és pontban, a testet pedig egy körben metszi. Mivel húrja ennek a körnek, e húr felezőmerőlegese, tehát az eredetileg szerkesztett merőleges -nek egy átmérőjét tartalmazza. Mivel a metsző síkot önkényesen vettük fel, kimondhatjuk, hogy az egyenesen átfektetett minden sík átmérőjű körben metszi a testet. Testünk ezért az átmérőjű gömbbel azonos. III. megoldás. Ha testünknek egy húrján át két síkot fektetünk (6. ábra), két körmetszethez, az egymást , pontokban metsző és körökhöz jutunk. 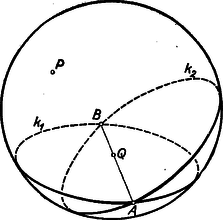 E két kör egy gömböt határoz meg (középpontja a két körközéppontban a körsíkokra emelt merőlegesek metszéspontja, s ezeknek van metszéspontjuk, mert felezőmerőleges síkjában vannak, és nem párhuzamosak). Legyen testünk felületén egy pont. Fektessünk egy síkot a ponton és az húrnak egy belső pontján át. Ez a sík a és kört négy pontban metszi, hiszen áthalad mindkét körnek belső pontján, a ponton. Ez a négy pont a gömb felületén egy kört határoz meg. A felvett sík körmetszete is áthalad e négy ponton, ez a két kör tehát azonos. Ezek szerint is felületén van, és minden, a ponton áthaladó sík által -ből kimetszett kör testünknek felületén helyezkedik el. Testünk ezért a gömbbel azonos. IV. megoldás. Legyen a testnek egy körmetszete (6. ábra), legyen ennek a körlemeznek belső pontja, legyen a test felületén, de nem a körön, legyen végül az a gömb, amelyik áthalad a ponton és tartalmazza a kört. A egyenesen átfektetett sík a kört és pontban metszi (hiszen tartalmazza a körnek belső pontját), továbbá testünket és a gömböt is körben metszi. E két kör azonos, mert , és közös pontjaik. E síkmetszetek azonosságából a test és a gömb azonossága következik. |