Feladat: 1954. évi Kürschák matematikaverseny 1. feladata Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Balatoni Ferenc ,  Bárdos András ,  Csiszár Imre ,  Kovács Imre ,  Vigassy József 
Füzet: 1955/április, 100 - 101. oldal  PDF  |  MathML 
Témakör(ök): Négyszögek geometriája, Ellipszis, mint kúpszelet, Háromszög-egyenlőtlenség alkalmazásai, Trigonometrikus függvények, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):Feladatok: 1955/január: 1954. évi Kürschák matematikaverseny 1. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megjegyzések: 1. Mivel a feladat négyszögről szól, az A, B, C, D pontoknak egymástól különbözőknek kell lenniök. Ezért téved, aki szerint a feladatnak azt kellene állítania, hogy az AB oldal nem nagyobb az AC átlónál, hiszen AB= =AC, ha B és C egybeesik (?).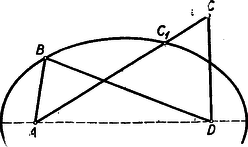
2. A következő okoskodás alátámasztja azt, hogy a feladat állítása helyes. Rajzoljunk ellipszist, amelynek fókuszai A és D, és amelyik áthalad a B ponton (1. ábra).

 
 
1. ábra
 

A feladat feltevéséből következik, hogy C ezen az ellipszisen kívül van, vagy esetleg rajta. Ezért az AC szakasznak egy C1 pontja az ellipszisen van, C1 esetleg azonos a C ponttal. Minthogy >>az ellipszisnek A-ból induló rádiuszvektora állandóan növekszik, amint végpontja az ellipszisen a nagytengely A-hoz közelebb eső végpontjától a D-hez közelebb eső végpont felé mozog<<, következik az, hogy AB kisebb AC1-nél, s így még inkább kisebb AC-nél. ‐ Ezt az okoskodást bizonyításnak nem nevezhetjük, hiszen az idézőjelek közé foglalt állítást a szemlélet alapján elhisszük ugyan, de bizonyítva nem látjuk. ‐ Bizonyítássá válik ez az okoskodás, ha ezt az állítást nemcsak kimondjuk, hanem bizonyítjuk is. Ennek kifogástalan elvégzése azonban elég körülményes feladat (hacsak nem éppen feladatunknak más megoldása alapján következtetünk ennek az állításnak helyességére). ‐ Az említett bizonyítás kevés munkával elvégezhető, ha a trigonometriát használjuk, és arra az előismeretre építünk, hogy pl. a cosinus-függvény 0∘ és 180∘ között állandóan fogy. Az ilyen bizonyítás eleminek és ötletesnek semmiképpen sem volna nevezhető.
 

I. megoldás. Tegyük fel, hogy állításunkkal ellentétben AB≥AC, hogy tehát az A pont a BC szakasz felezőmerőlegesén, vagy pedig ennek C felőli oldalán helyezkedik el (2. ábra).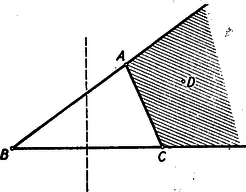
 
 
2. ábra
 

Mivel az ABCD négyszög konvex, következik, hogy a D pont az AB oldalegyenesnek C felőli oldalán, a BC oldalegyenesnek A felőli oldalán, végül az AC átlóegyenesnek B-vel átellenes oldalán van. A D pont tehát annak (az ábrán vonalkázott) tartománynak belsejében van, amelyet megkapunk, ha az ABC∢ tartományából az ABC háromszöget levágjuk. Ennek a tartománynak a belseje azonban egészben a BC szakasz felezőmerőlegesének C felőli oldalán van, hiszen határvonalainak pontjai közül legfeljebb csak A lehet a felezőmerőlegesen. Ezért a D pont is ebben a félsíkban van, és BD>CD. Ezt az egyenlőtlenséget az igaznak elfogadott egyenlőtlenséggel összegezve AB+BD> >AC+CD adódik, ami ellentmond a feladat kirovásának. Ez az ellentmondás feltevésünk lehetetlenségét és a feladat állításának helyességét bizonyítja.
 

II. megoldás. Ha BD>CD, akkor ebből és AB+BD≤AC+CD fennállásából (kivonással) következik, hogy AB<AC. Ezért a bizonyításnál jogosan szorítkozhatunk arra az esetre, amidőn BD≤CD (3. 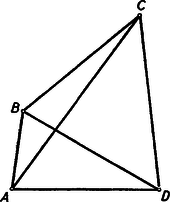ábra).
 
 
3. ábra
 

Ebben az esetben ‐ hivatkozva arra a tételre, hogy a háromszögben nagyobb oldallal szemben nagyobb szög van ‐ a BCD▵-ből adódik, hogy BCD∢≤DBC∢. Így tehát BCA∢<ABC∢, hiszen az előző egyenlőtlenség baloldalán szereplő szöget csökkentettük, a jobboldalon állót meg növeltük. Az utóbbi egyenlőtlenségből azonban ‐ a már idézett tételt az ABC▵-re alkalmazva ‐ adódik, hogy AB<AC.
 

III. megoldás. Ismeretes (és a háromszög oldalaira vonatkozó egyenlőtlenségből nyomban következik), hogy egy konvex négyszög két átellenes oldalának összege az átlók összegénél kisebb, esetünkben tehát AB+CD<AC+BD. A feladat feltevése szerint AB+BD≤AC+CD. Ezeket az egyenlőtlenségeket összegezve, rendezés után 2⋅AB<2⋅AC adódik, ami állításunkat bizonyítja.