Kezdőlap


Feladat:	1952. évi Kürschák matematikaverseny 3. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Füzet:	1953/január, 8 - 12. oldal		PDF \| MathML
Témakör(ök):	Háromszögek nevezetes tételei, Háromszögek egybevágósága, Háromszögek hasonlósága, Trigonometrikus függvények, Elsőfokú (és arra visszavezethető) egyenlőtlenségek, Trigonometriai azonosságok, Háromszög-egyenlőtlenség alkalmazásai, Egyéb sokszögek geometriája, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):	Feladatok: 1953/január: 1952. évi Kürschák matematikaverseny 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Húzzunk párhuzamosakat az $A_{1}$ , $B_{1}$ , $C_{1}$ pontokon át rendre az $A B$ , $B C$ , $C A$ oldalakkal (7. ábra). E párhuzamosak a $C A$ , $A B$ , $B C$ oldalakat rendre $B_{2}$ , $C_{2}$ , $A_{2}$ pontokban metszik. Az így kapott $A C_{2} B_{1}$ , $C_{1} B A_{2}$ , $B_{2} A_{1} C$ háromszögek oldalaik párhuzamossága miatt hasonlók az $A B C Δ$ -höz.

7. ábra

E háromszögek egymással egybevágók, ugyanis

\begin{matrix} A_{1} C = (1 - λ) \cdot B C, B_{1} A = (1 - λ) \cdot C A, C_{1} B = (1 - λ) \cdot A B \end{matrix}

miatt egy-egy oldaluk az eredeti háromszög megfelelő oldalának ugyanannyiszorosa. Az egybevágóságból következik, hogy

\begin{matrix} A_{1} B_{2} = C_{2} A, B_{1} C_{2} = A_{2} B, C_{1} A_{2} = B_{2} C . \end{matrix}

Ebből pedig az adódik, hogy az

A_{1} B_{2} B_{1} C_{2} C_{1} A_{2}

hatszög kerülete az

A C_{1}

B A_{1}

C B_{1}

távolságok összegével, vagyis az eredeti háromszög oldalai

λ

-szorosainak összegével, tehát az

A B C Δ

kerületének

λ

-szorosával egyenlő.
A feladat állítása most már abból következik, hogy az

A_{1} B_{1} C_{1} Δ

kerülete a szerepeltetett hatszög kerületénél kisebb. Hiszen e háromszög egy-egy oldala kisebb a hatszög két-két oldalának összegénél.

Megjegyzés: Megoldásunk kihasználta, hogy a szereplő hatszög csúcsai mind különböző pontok. Ez nem következik be, ha

λ = \frac{1}{2}

, amikor is

A_{1} \equiv A_{2}

B_{1} \equiv B_{2}

C_{1} \equiv C_{2}

, s akkor sem, ha

λ = 1

, amikor viszont

A_{1} \equiv B_{2}

B_{1} \equiv C_{2}

C_{1} \equiv A_{2}

. A feladat állítása sem helyes ebben a két esetben, hiszen az

A_{1} B_{1} C_{1} Δ

kerülete mindkét esetben éppen egyenlő az

A B C Δ

kerületének

λ

-szorosával.
Kihasználta okoskodásunk azt a tényt is, hogy a

C_{2}

A_{2}

B_{2}

pontok rendre az

A C_{1}

B A_{1}

C B_{1}

távolságok belsejében vannak. Hiszen különben nem volna pl. a hatszög

A_{1} B_{2}

és

C_{2} C_{1}

oldalának összege az

A C_{1}

távolsággal egyenlő. A mondott tény bekövetkezése annak következménye, hogy

λ > \frac{1}{2}

, azaz

1 - λ < λ

. Ugyanis pl.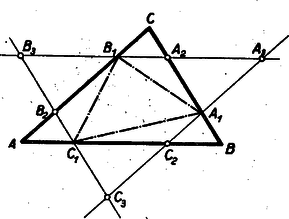

\begin{matrix} A C_{2} = (1 - λ) \cdot A B < λ \cdot A B = A C_{1} . \end{matrix}

Nem is igaz a feladat állítása, ha

0 < λ < \frac{1}{2}

. Ezt a következőképpen bizonyítjuk: Az

A_{1}

B_{1}

C_{1}

pontokon át párhuzamosakat húzunk rendre a

C A

A B

B C

oldalakkal (8. ábra).

8. ábra

E párhuzamosak az

A B

B C

C A

oldalakat rendre

C_{2}

A_{2}

B_{2}

pontokban metszik, s együttesen az

A_{3} B_{3} C_{3} Δ

-et határolják. Az

A C_{1} B_{2}

C_{2} B A_{1}

B_{1} A_{2} C

háromszögek oldalaik párhuzamossága miatt hasonlók az eredeti háromszöghöz, s egymással egybevágók is, mert mindegyiküknek egy-egy oldala az

A B C Δ

megfelelő oldalának

λ

-szorosa. Így tehát

\begin{matrix} B_{1} A_{2} = λ \cdot A B, C_{1} B_{2} = λ \cdot B C, A_{1} C_{2} = λ \cdot C A . \end{matrix}

Tudjuk most azt is, hogy az

A_{2}

B_{2}

C_{2}

pontok rendre a

B A_{1}

C B_{1}

A C_{1}

távolságokon kívül vannak, hogy tehát az

A_{3} B_{3} C_{3} Δ

csúcsai az eredeti háromszögön kívül helyezkednek el. Az előbbi mintára belátjuk, hogy az

A_{3} A_{2} A_{1}

B_{1} B_{3} B_{2}

C_{2} C_{1} C_{3}

háromszögek hasonlók az eredeti háromszöghöz, s egymással egybevágók, mert

A_{1} A_{2}

B_{1} B_{2}

C_{1} C_{2}

oldalaik az

A B C Δ

megfelelő oldalainak

(1 - 2 λ)

-szorosai. Így tehát

\begin{matrix} A_{2} A_{3} = B_{3} B_{1}, B_{2} B_{3} = C_{3} C_{1}, C_{2} C_{3} = A_{3} A_{1} . \end{matrix}

A_{1} B_{1} A_{3}

B_{1} C_{1} B_{3}

C_{1} A_{1} C_{3}

háromszögek egy-egy oldalára felírva, hogy a másik két oldal különbségénél nagyobb:

\begin{matrix} A_{1} B_{1} > B_{1} A_{2} + A_{2} A_{3} - A_{3} A_{1}, \\ B_{1} C_{1} > C_{1} B_{2} + B_{2} B_{3} - B_{3} B_{1}, \\ C_{1} A_{1} > A_{1} C_{2} + C_{2} C_{3} - C_{3} C_{1} . \end{matrix}

Ezeknek az egyenlőtlenségeknek összege a fenti egyenlőségek figyelembe vételével:

\begin{matrix} A_{1} B_{1} + B_{1} C_{1} + C_{1} A_{1} > B_{1} A_{2} + C_{1} B_{2} + A_{1} C_{2} . \end{matrix}

Ez pedig fentebbi megállapításunk értelmében éppen azt mondja ki, hogy az

A_{1} B_{1} C_{1} Δ

kerülete az

A B C Δ

kerületének

λ

-szorosánál nagyobb.
Akkor sem teljesül a feladat állítása, ha

λ > 1

, mikor is az

A_{1}

B_{1}

C_{1}

pontok az

A B C Δ

oldalainak meghosszabbítására kerülnek. Ezt a következőképpen látjuk be: Az

A_{1}

B_{1}

C_{1}

pontokon át párhuzamosakat húzunk rendre az

A B

B C

C A

oldalakkal (9. ábra).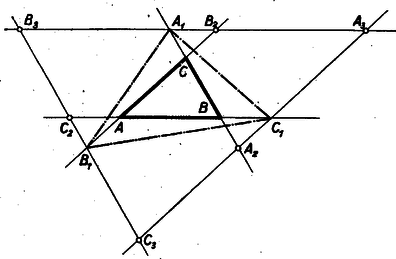

9. ábra

E párhuzamosak a

C A

A B

B C

oldalakat rendre

B_{2}

C_{2}

A_{2}

pontokban metszik, s együttesen az

A_{3} B_{3} C_{3} Δ

-et határolják. Az

A C_{2} B_{1}

C_{1} B A_{2}

B_{2} A_{1} C

háromszögek oldalaik párhuzamossága miatt hasonlók az eredeti háromszöghöz, s egymással egybevágók, mert egy-egy oldaluk az

A B C Δ

megfelelő oldalának

(λ - 1)

-szerese. Ebből az egybevágóságból következik, hogy

A_{2} B = C A_{1}

B_{2} C = A B_{1}

C_{2} A = B C_{1}

, hogy tehát a

C A_{2}

A B_{2}

B C_{2}

távolságok is

λ

-szorosai az

A B C Δ

oldalainak. Minthogy

A B_{2} A_{3} C_{1}

B C_{2} B_{3} A_{1}

és

C A_{2} C_{3} B_{1}

paralelogramma, megállapításainkból következik, hogy az

A_{3} B_{3} C_{3} Δ

oldalait az ezeken elhelyezkedő két-két pont olyan három‐három távolságra darabolja, amelyek az

A B C Δ

egy-egy oldalának sorjában

λ

-szorosai,

(λ - 1)

-szeresei és

λ

-szorosai. Így tehát az

A_{1} B_{1} C_{1} Δ

csúcsai úgy helyezkednek el az

A_{3} B_{3} C_{3} Δ

oldalain, hogy

\begin{matrix} B_{3} A_{1} : B_{3} A_{3} = C_{3} B_{1} : C_{3} B_{3} = A_{3} C_{1} : A_{3} C_{3}, \end{matrix}

hiszen ezeknek az arányoknak mindegyike a

λ : (3 λ - 1)

aránnyal egyenlő. Minthogy ennek az aránynak értéke

λ > 1

folytán

\frac{1}{2}

-nél kisebb, azért előzőleg bizonyított állításunk e háromszögekre teljesül. Tudjuk tehát, hogy az

A_{1} B_{1} C_{1} Δ

kerülete nagyobb a

B_{3} A_{1}

C_{3} B_{1}

A_{3} C_{1}

távolságok összegénél, azaz az

A B C Δ

kerületének

λ

-szorosánál.
Megjegyezhetjük még, hogy

λ \leq 0

esetben a feladat állítása eleve nem teljesülhet, hiszen egy háromszög kerülete csak pozitív lehet.
Összefoglalva az e megjegyzésben mondottakat megállapítjuk, hogy a feladat

1 / 2 < λ < 1

megkötése lényeges. Ha e megkötés nem teljesül, a feladat állítása soha sem helyes.

II. megoldás: Ha a

γ_{1}

és

γ_{2}

szög

0

-nál nagyobb és

180^{\circ}

-nál kisebb, akkor

\begin{matrix} sin (γ_{1} + γ_{2}) < sin γ_{1} + sin γ_{2}, \end{matrix}

hiszen a baloldalt növeljük, ha azt

sin γ_{1} cos γ_{2} + cos γ_{1} sin γ_{2}

alakban írva a pozitív sinus-tényezők cosinus-együtthatóinak helyébe azoknál nagyobb

1

-et írunk.
Ha továbbá egy ugyancsak

0

-nál nagyobb és

180^{\circ}

-nál kisebb

δ

szöget szerepeltetünk, akkor az előző egyenlőtlenséget a pozitív

sin δ

-val szorozva

\begin{matrix} sin (δ + γ_{1}) sin γ_{2} + sin (δ - γ_{2}) sin γ_{1} < sin δ (sin γ_{1} + sin γ_{2}) \end{matrix}

adódik. Ugyanis (a szereplő szögösszegek és szögkülönbségek függvényeit a tagok függvényeivel fejezve ki)

\begin{matrix} sin δ sin (γ_{1} + γ_{2}) = sin (δ + γ_{1}) sin γ_{2} + sin (δ - γ_{2}) sin γ_{1} \end{matrix}

azonosan teljesül. Így tehát utolsó egyenlőtlenségünket a pozitív

sin γ_{1} sin γ_{2}

szorzattal osztva

\begin{matrix} \frac{sin (δ + γ_{1})}{sin γ_{1}} + \frac{sin (δ - γ_{2})}{sin γ_{2}} < \frac{sin δ}{sin γ_{1}} + \frac{sin δ}{sin γ_{2}} . \end{matrix}

Tekintsünk egy

a

b

c

oldalú háromszöget, melyet egy

d

hosszúságú távolság egy

a

d

c_{1}

és egy

b

d

c_{2}

oldalú háromszögre vág (10. ábra).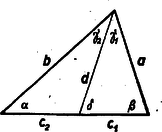

10. ábra

Ezekre fennáll a

\begin{matrix} \frac{d}{c_{1}} + \frac{d}{c_{2}} < \frac{a}{c_{1}} + \frac{b}{c_{2}} \end{matrix}

egyenlőtlenség. Ugyanis a sinus-tétel szerint ez az előbbi egyenlőtlenséggel azonos, ha ábránk szögjelöléseit használjuk, hiszen e szögekre

\begin{matrix} a = δ - γ_{2}, β = π - (δ + γ_{1}) . \end{matrix}

Ha utolsó egyenlőtlenségünket

(\frac{1}{c_{1}} + \frac{1}{c_{2}})

-vel osztjuk és a

μ = \frac{c_{1}}{c_{1} + c_{2}}

jelölést használjuk, akkor a

\begin{matrix} d < μ b + (1 - μ) a \end{matrix}

egyenlőtlenséghez jutunk.
Tekintsünk egy

A_{2} B_{2} C_{2} Δ

-et (11. ábra), melynek oldalain az

A_{3}

B_{3}

C_{3}

pontok úgy helyezkednek el, hogy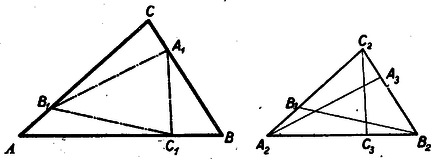

\begin{matrix} A_{3} C_{2} : B_{2} C_{2} = B_{3} A_{2} : C_{2} A_{2} = C_{3} B_{2} : A_{2} B_{2} . \end{matrix}

11. ábra

Állítjuk, hogy az

A_{2} A_{3}

B_{2} B_{3}

C_{2} C_{3}

távolságok összege az

A_{3} B_{3} C_{3}

kerületénél kisebb. Ha ugyanis a fenti arányok közös értékét

μ

-vel jelöljük, akkor előző megállapításunk értelmében

\begin{matrix} A_{2} A_{3} < μ A_{2} B_{2} + (1 - μ) C_{2} A_{2}, \\ B_{2} B_{3} < μ B_{2} C_{2} + (1 - μ) A_{2} B_{2}, \\ C_{2} C_{3} < μ C_{2} A_{2} + (1 - μ) B_{2} C_{2} . \end{matrix}

Ezeknek az egyenlőtlenségeknek összege éppen állításunkat adja.
Tekintsük végül magát a feladatban leírt alakzatot. Legyen az

A_{2} B_{2} C_{2} Δ

hasonló az

A B C Δ

-höz, s oldalai legyenek az

A B C Δ

oldalainak

λ

-szorosai, tehát az

A_{2} B_{2}

B_{2} C_{2}

C_{2} A_{2}

oldalak rendre az

A C_{1}

B A_{1}

C B_{1}

távolságokkal egyenlők. Ezekre az oldalakra felmérjük a

C_{2} A_{3} = C A_{1}

A_{2} B_{3} = A B_{1}

B_{2} C_{2} = B C_{1}

távolságokat, amit

1 - λ < λ

miatt megtehetünk. Ezzel biztosítottuk, hogy az

A_{2} C_{2} A_{3}

B_{2} A_{2} B_{3}

C_{2} B_{2} C_{3}

háromszögek rendre egybevágók a

B_{1} C A_{1}

C_{1} A B_{1}

A_{1} B C_{1}

háromszögekkel, s így az

A_{2} A_{3}

B_{2} B_{3}

C_{2} C_{3}

távolságok összege az

A_{1} B_{1} C_{1} Δ

kerületével egyenlő. Minthogy az

A_{3}

B_{3}

C_{3}

pontok felvételénél az

A_{2} B_{2} C_{2} Δ

oldalaira ezeknek az oldalaknak ugyanannyiszorosát, t. i.

μ = \frac{1 - λ}{λ}

-szorosát mértük fel, teljesülnek előzőleg bizonyított állításunknak feltételei. E szerint tehát az

A_{2} A_{3}

B_{2} B_{3}

C_{2} C_{3}

távolságok összege az

A_{2} B_{2} C_{2} Δ

kerületénél, vagyis az

A_{1} B_{1} C_{1} Δ

kerülete az

A B C Δ

kerületének

λ

-szorosánál kisebb.

Megjegyzés: Nem nehéz e második megoldást úgy alakítani, hogy az

\frac{1}{2} < λ < 1

kirovás szükségessége is kiolvasható legyen. Elegendő ugyanis a megoldásban szereplő első egyenlőtlenséghez hozzáfűzni, hogy amennyiben a

γ_{1}

és

γ_{2}

szögek

- 180^{\circ}

és

180^{\circ}

közé esnek, s összegük pozitív, úgy ez az első egyenlőtlenség csak akkor teljesül, ha a

γ_{1}

és

γ_{2}

szögek mindegyike pozitív. Ebből a megállapításból kiindulva megoldásunk gondolatmenetének változatlan megtartása (s előjeles távolságok és szögek használata) mellett a mondott eredményhez juthatunk, ezt azonban itt nem részletezzük.