| Feladat: | 1952. évi Kürschák matematikaverseny 2. feladata | Korcsoport: 18- | Nehézségi fok: nehéz |
| Megoldó(k): | Horváth Ákos , Kántor Sándor , Nagy Tibor | ||
| Füzet: | 1953/január, 5 - 8. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Természetes számok, Részhalmazok, Számhalmazok, Halmazok számossága, Elsőfokú (és arra visszavezethető) egyenlőtlenségek, Kör geometriája, Kürschák József (korábban Eötvös Loránd) | ||
| Hivatkozás(ok): | Feladatok: 1953/január: 1952. évi Kürschák matematikaverseny 2. feladata | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. I. megoldás: Az első egész számot három csoportba osztjuk: Legyen a kiválasztott számok legkisebbike. Ha szerepel a kiválasztott számok között olyan, amelyik -nél nagyobb s -nél kisebb, akkor és ez a szám kielégíti a feladat kívánalmát. Ha viszont a mondott számoknak egyike sem szerepel a kiválasztottak között, akkor és szükségképpen szerepel közöttük, mert különben a mondott számokat közrefogó két szomszédos kiválasztott számnak különbsége feltevésünkkel ellentétben -nél nagyobb volna. Bizonyos, hogy van két ilyen közrefogó szomszédos szám, hiszen maga a mondott számoknál kisebb, s nagyobbnak is kell lennie a kiválasztott számok között, minthogy -tól kezdve -ig bezárólag összesen csak szám van. Ha viszont , és szerepel a kiválasztott számok között, akkor bármely negyedik szám e három valamelyikével együtt megfelel a feladat kívánalmának. Hiszen -nál kisebb szám nincs a kiválasztottak között, az -nál nagyobb és -nél kisebb számoknak -nel alkotott különbségük, az -nél nagyobb és -nél kisebb számoknak -val alkotott különbségük, az -nél nagyobb és -nél nem nagyobb számoknak pedig -nel alkotott különbségük -nél nagyobb s egyben -nél kisebb. Minthogy pedig esetben , található a felsorolt háromtól különböző negyedik kiválasztott szám. Így tehát minden esetben eljutottunk a feladat kívánalmát kielégítő számpárhoz. Ha az , számok egyike szerepel a kiválasztottak között, úgy ennek és -nek különbsége -nél nagyobb, de -nél kisebb. Ha viszont a mondott számok egyike sem szerepel, akkor az Két szám akkor elégíti ki a feladat kívánalmát, ha a kisebbiktől növekvő számok irányában haladó, s a nagyobbikhoz vezető körívnek hossza harmadkörnél nagyobb s a kör kétharmadánál kisebb. Ez a megkötés azonban egy körívre s az azt teljes körré kiegészítő körívre csak egyszerre teljesülhet, és ha két egymást teljes körré kiegészítő körívnek mindegyike nagyobb a harmadkörnél, akkor már eleve kisebbek a kör kétharmadánál. Így tehát két szám akkor elégíti ki a feladat kívánalmát, ha a két számot összekötő mindkét körív nagyobb a harmadkörnél. Meggondolásaink alapján a feladatnak a következő új alakot adhatjuk: Egy kör kerületén egyenlő közökkel pont helyezkedik el, s ezek közül kiválasztunk darabot. Bizonyítandó, hogy mindig van a kiválasztott pontok között kettő, melyeket két, a harmadkörnél nagyobb körív köt össze. Vizsgáljuk, hogyan lehet a pont közül egyeseket kiválasztani anélkül, hogy volna közöttük kettő, melyeket két, a harmadkörnél hosszabb körív köt össze. Ez a tilalom akként is szövegezhető, hogy a kiválasztott pontokkal szemben elhelyezkedő harmadkörívek belsejéből nem szabad pontot kiválasztanunk. Ha a legnagyobb szabad körív harmadkör, akkor csak kiválasztott pont szerepelhet (6. ábra). 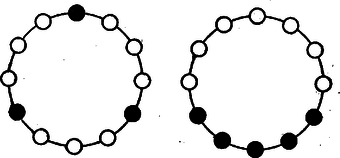 Ilyenkor ugyanis bizonyosan van egy szabad harmadkörív. Ennek végpontjai, mint kiválasztott pontok, a kiegészítő kétharmadív belső pontjainak kiválasztását is tiltják, egyedül e kétharmadív középpontjának kiválasztását nem. Ennek a középpontnak kell is szerepelnie a kiválasztott pontok között, mert különben nem harmadkör volna a szabad körívek legnagyobbika. Ha viszont a legnagyobb szabad körív a körnek kétharmada, vagy még nagyobb, akkor a kiválasztott pontok egy harmadkörön helyezkednek el, ennek végpontjait is beleértve. Minthogy egy harmadköríven végpontjaival együtt pont van, ilyenkor legfeljebb csak kiválasztott pont szerepelhet. Akár mind e pontokat kiválaszthatjuk, a tilalmat akkor sem hágjuk át. Mivel nagyobb -nél és feltevés mellett -nál is, azért pontot nem lehet a tilalom áthágása nélkül kiválasztani. Megoldásunk a feladat állításán túlmenően a következő eredményhez is elvezet: Minden megengedett kiválasztásnál: 1) vagy három , , alakú szám szerepel, 2) vagy egymást követő szám szerepel, 3) vagy együttesen olyan szám szerepel, amelyeknek egyik csoportja -hez csatlakozó s egymást követő, másik csoportja -hez csatlakozó s egymást követő számokat tartalmaz, 4) vagy pedig csak egyesek szerepelnek az előző két eset valamelyikében megadott számok közül. Felesleges volna részletezni, hogy ez valóban a feladat átírása. Ha a könyvtár kapusa az első látogató érkezésekor a könyvtár óráját déli -re állítja vissza, akkor nyilván csak azt teszi lehetővé, hogy esetleg még többen látogathassák aznap a könyvtárt. Feltehetjük tehát, hogy az első látogató pontosan -kor érkezik. A következőkben három esetet különböztetünk meg. Először avval az esettel foglalkozunk, hogy pontosan órakor és pontosan órakor is érkezik egy-egy látogató. Ekkor bizonyos, hogy többen nem is járnak a könyvtárban. Hiszen és között nem érkezhetik senki sem, mert az -kor biztosan aludna, s így álmát megzavarnák. Viszont és , valamint és között azért nem jöhet be senki sem, mert akkor alszik a -kor érkező, ill. az -kor érkező látogató. Ebben az esetben tehát látogató van. Másodszor feltesszük, hogy pontosan órakor érkezik látogató, de -kor nem. Ekkor bizonyos, hogy óra után senki sem érkezik. Ugyanis és között a -kor érkező, viszont és között az -kor érkező látogató alszik. Ebben az esetben tehát minden látogató -től kezdve óráig bezárólag érkezik, s így legfeljebb látogató van. Végül harmadszor feltesszük hogy pontosan órakor nem érkezik látogató. Szemeljük ki ekkor azt a látogatót, aki utoljára érkezett óra előtt (lehet, hogy az első látogatót kell így kiszemelnünk). A kiszemelt látogató érkezésétől számított kétórás időközön belül újabb látogató nem érkezhet, hiszen ez csak elalvása előtt volna lehetséges, viszont sem érkezésétől óráig, sem órakor nem érkezik senki sem, és órától a kiszemelt látogató elalvásáig terjedő időben (ha ugyan nem az első látogatót magát szemeltük ki), már alszik az első látogató. Ezek szerint a mondott két órás időközön belül belépési lehetőség kihasználatlanul kell, hogy maradjon, a látogatók a megengedett lehetőségből csak a többit használhatták ki. Ebben az esetben tehát ugyancsak legfeljebb látogató van. Egybevetve megállapítjuk, hogy mindenképpen csak legfeljebb ember járhat egy napon a könyvtárban. Nyilván helyes marad okoskodásunk akkor is, ha az órát nem , hanem percre osztjuk fel. Egyedül az lényeges, hogy a helyébe lépő ne legyen -nál kisebb, vagyis hogy az feltétel teljesüljön. |