Kezdőlap


Feladat:	1952. évi Kürschák matematikaverseny 1. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Horváth Ákos , Kálmán Lajos , Kántor Sándor , Nagy Tibor
Füzet:	1953/január, 2 - 5. oldal		PDF \| MathML
Témakör(ök):	Kör geometriája, Háromszögek nevezetes tételei, Háromszög-egyenlőtlenség alkalmazásai, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):	Feladatok: 1953/január: 1952. évi Kürschák matematikaverseny 1. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Jelölje $O_{1}$ , $O_{2}$ , $O_{3}$ a három adott kör középpontját, s legyen közülük $O_{2}$ a másik kettő között. A három kör sugarát rendre $r_{1}$ , $r_{2}$ , $r_{3}$ jelöli. A negyedik kör középpontja és sugara legyen 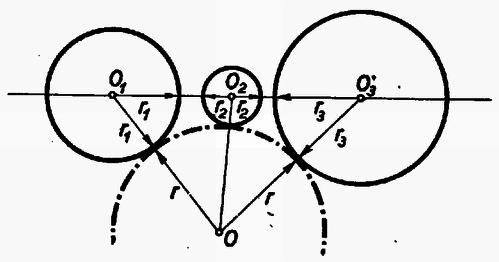$O$ és $r$ .

1. ábra

A negyedik kör nem lehet egyik adott körnek sem a belsejében, mert akkor nem érinthetné a másik kettőt is. Nem kell foglalkoznunk avval az esettel sem, midőn a három adott körnek valamelyike a negyedik kört belülről érinti, mert ez esetben a negyedik kör sugara a belülről érintő kör sugaránál nagyobb, s így nem lehet a négy körsugár közül a legkisebb. Ezért csak avval az esettel foglalkozunk, amikor a negyedik kör kívülről érinti a három adott kört (1. ábra).
Az

O O_{1} O_{3} Δ

oldalaira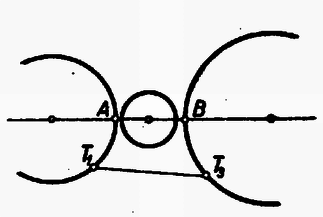

\begin{matrix} O O_{1} + O O_{3} > O_{1} O_{3} . \end{matrix}

Minthogy a körök kívülről érintik egymást,

O O_{1} = r + r_{1}

és

O O_{3} = r + r_{3}

. Mivel a három adott kör közül nincs kettőnek közös belső pontja,

O_{1} O_{3} \geq r_{1} + 2 r_{2} + r_{3}

, hiszen az

O_{1} O_{3}

szakasz tartalmazza a két szélső kör sugarát s a középsőnek átmérőjét, s e sugarak és az átmérő egymást még részben sem fedik. Igaz ez akkor is, ha a középső kör érinti a két szélsőnek valamelyikét, vagy akár mindkettőt is. Az utóbbi esetben az egyenlőség jele érvényes.

Fenti egyenlőtlenségünk alapján tehát

\begin{matrix} r_{1} + 2 r + r_{3} > r_{1} + 2 r_{2} + r_{3}, \end{matrix}

amiből

r > r_{2}

adódik. Az

r

sugár tehát

r_{1}

r_{2}

r_{3}

mindegyikénél kisebb nem lehet.

II. megoldás: Jelölje

A

és

B

a két szélső körnek egymáshoz legközelebb eső pontjait, tehát a centrális egyenesnek s a két szélső körnek egy-egy metszéspontját (2. ábra).

2. ábra

Minthogy az

A B

távolság a középső kör átmérőjét tartalmazza,

\begin{matrix} A B \geq 2 r_{2} . \end{matrix}

Jelölje

T_{1}

és

T_{3}

a negyedik körnek s a két szélső körnek közös pontjait. Minthogy

T_{1} T_{3}

a negyedik körnek húrja,

\begin{matrix} 2 r \geq T_{1} T_{3} . \end{matrix}

A

és

B

megválasztásából viszont következik, hogy

\begin{matrix} T_{1} T_{3} \geq A B . \end{matrix}

Egyenlőtlenségeink összevetéséből

\begin{matrix} 2 r \geq 2 r_{2}, \end{matrix}

azaz

r \geq r_{2}

adódik. Ez pedig a feladat állítását igazolja.

III. megoldás: Emeljünk a centrális egyenesnek s a középső körnek metszéspontjaiban merőlegeseket a centrálisra (3. ábra).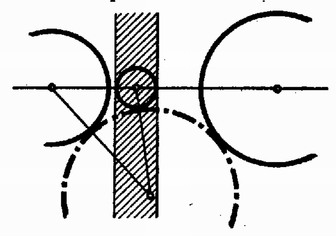

3. ábra

E két párhuzamos egyenes egy síksávot fog közre. A három adott kör közül a két szélső ennek a sávnak más-más oldalán van. Minthogy a negyedik körnek van közös pontja mindkét szélső körrel, azért tudjuk, hogy a negyedik kör a sávnak mindkét partját eléri, átmérője tehát a sáv szélességénél, sugara pedig annak felénél, vagyis a középső kör sugaránál kisebb nem lehet.

IV. megoldás: Keressük az olyan negyedik körnek középpontját, amelyiknek van a két szélső körrel egy-egy közös pontja, s amelyiknek sugara a középső kör sugaránál kisebb.
Ha a két szélső kör sugarát a középső kör sugarával megnöveljük, olyan köröket kapunk, amelyeknek mindegyike belsejében kell, hogy tartalmazza a kívánt tulajdonságú negyedik körnek középpontját (4. ábra).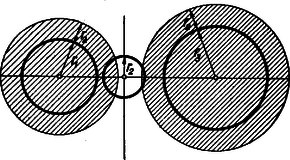

4. ábra

Hiszen e körök valamelyikén kívül lévő pont körül

r_{2}

-nél kisebb sugárral írt kör nem éri a megfelelő szélső kört.
Emeljünk a középső kör középpontjában merőlegest a centrális egyenesre. Minthogy éppen a középső kör sugarával növeltük az előbb a sugarakat, azért a megnövelt körök a most szerkesztett merőleges egyenesnek más-más oldalán vannak. A megnövelt köröknek tehát nincs közös belső pontjuk, s így kívánt tulajdonságú negyedik kör sincs.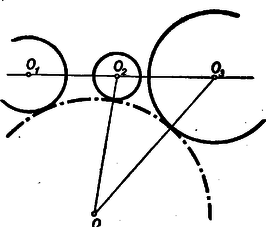

V. megoldás: Kössük össze a negyedik kör

O

középpontját a középső kör

O_{2}

középpontjával. Az

O O_{2} O_{1} ∢

és

O O_{2} O_{3} ∢

összege

180^{\circ}

, s így mindkettő nem lehet

90^{\circ}

-nál kisebb (5. ábra).

5. ábra

Legyen pl.

O O_{2} O_{3} ∢ \geq 90^{\circ}

. Ekkor az

O O_{2} O_{3} Δ

-ben ez a legnagyobb szög, s ezért

O O_{3}

a háromszög legnagyobb oldala, tehát

\begin{matrix} O O_{3} > O_{2} O_{3} . \end{matrix}

Minthogy az

O

és

O_{3}

középpontú köröknek van közös pontjuk,

O O_{3} \leq r + r_{3}

. Mivel az

O_{2}

és

O_{3}

középpontú köröknek nincs közös belső pontjuk,

O_{2} O_{3} \geq r_{2} + r_{3}

. Így tehát

\begin{matrix} r + r_{3} > r_{2} + r_{3}, \end{matrix}

azaz

r > r_{2}

, tehát

r

nem lehet

r_{1}

r_{2}

r_{3}

mindegyikénél kisebb.

Megjegyzések: 1. Végső következtetésünk mindegyik megoldásnál az volt, hogy

r

nem lehet a legkisebb a négy körsugár közül, azaz nem lehet a másik három mindegyikénél kisebb. Megoldásaink azt is bizonyítják, hogy

r

nem lehet

r_{2}

-nél kisebb sem.
2. Az is igaz, hogy

r

nem lehet a négy körsugár közül még a legkisebbek között sem, azaz van a másik három sugár között

r

-nél kisebb. Sőt bizonyos, hogy

r_{2}

kisebb

r

-nél. Ezt az első és ötödik megoldás ki is mondja. A többi három megoldás okoskodása csekély toldással ugyancsak elvezet ehhez az eredményhez.
3. Az első megoldás használta csak ki azt, hogy a negyedik kör érinti a két szélsőt. A többi arra épített, hogy a negyedik körnek van közös pontja a szélső körökkel, tehát azt is megengedte, hogy a negyedik kör messe a szélsőket. Az első megoldás lényegtelen módosítással ugyanilyenné alakítható.
4. Csak az első és ötödik megoldás használta ki valamennyire azt, hogy a negyedik kör érinti a középsőt. Ez abban nyilvánult, hogy e megoldások

O O_{1} O_{3}

, ill.

O O_{2} O_{3}

háromszögről szóltak, tehát feltételezték hogy

O

nincs rajt a centrális egyenesen. Ez valóban nem következhetik be, ha a negyedik körnek van közös pontja a szélső körökkel, és érinti a középsőt. Így érthető az is, hogy éppen ezt a két megoldást kellett 2. megjegyzésünkben kiemelnünk.
5. A második megoldásból kiolvashatjuk, hogy

r = r_{2}

csak akkor állhat fenn, ha mindenütt az egyenlőség jele volt érvényes: ha tehát

A B

átmérője a középső körnek, ha

T_{1} T_{3}

átmérője a negyedik körnek, ha továbbá

T_{1} T_{3}

és

A B

azonos. Ez pedig azt jelenti, hogy a középső kör érinti a két szélsőt, és a negyedik körrel azonos. Ugyanehhez az eredményhez a többi megoldás alapján is eljuthatunk.
6. Megjegyzéseinket összefoglalva a feladat állításának következő általánosítását mondhatjuk ki: Három kör közül kettőnek-kettőnek nincs közös belső pontja, s középpontjaik egy egyenesen vannak; ha egy negyedik körnek van közös pontja e három kör közül a két szélsőnek mindegyikével, akkor e negyedik körnek sugara nem lehet a középső kör sugaránál kisebb, és egyenlő is csak akkor lehet azzal, ha a középső kör érinti a két szélsőt, s ha továbbá a negyedik kör a középső körrel azonos.