Kezdőlap


Feladat:	1951. évi Kürschák matematikaverseny 3. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Fáy Árpád , Kálmán Lajos , Seregély József , Szekerka Pál
Füzet:	1952/február, 7 - 11. oldal		PDF \| MathML
Témakör(ök):	Sík geometriája, Elsőfokú (és arra visszavezethető) egyenlőtlenségek, Egyenesek egyenlete, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):	Feladatok: 1952/február: 1951. évi Kürschák matematikaverseny 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Két félsík elhelyezése után az 5. ábrában feltüntetett 4 helyzet állhat elő, ahol a határegyenes sraffozott oldala jelenti a félsíkot.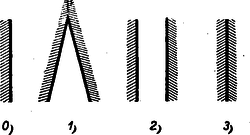

5. ábra

A (0) helyzetben a két határegyenes párhuzamos és az egyik félsík a másik félsíkot teljesen elfedi, tehát ez utóbbi máris felesleges. Ezzel a helyzettel már nem kell foglalkoznunk.
Tehát csak az (1), (2) és (3) eseteket kell a továbbiakban figyelembe venni, mikor egy ék, egy síksáv, illetőleg egy egyenes (a két félsík közös határegyenese) marad fedetlenül.
A harmadik félsík hozzáillesztésével (1)-ből előállhat az I/a, I/b és I/c helyzet, (2)-ből a II. helyzet és (3)-ból a III. helyzet (6. ábra).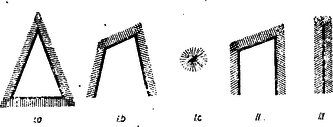

6. ábra

Az I/c eset (amidőn a 3 határegyenes egy pontban metszi egymást és így csak az egyetlen pont marad feladatunk értelmében fedetlen) az egyik félsíknak egy tetszésszerinti kis elhúzásával mindig visszavezethető az I/a esetre. Ugyanígy a III. helyzet is visszavezethető a II. helyzetre a közös határegyenessel bíró két félsíknak egy tetszésszerinti kicsiny széthúzásával. A negyedik félsík elhelyezésénél tehát már csak az I/a, I/b és II. esetekkel kell foglalkoznunk.
A fedetlen részeket teljesen lefedő negyedik félsík határegyenese vagy párhuzamos az első 3 sík valamelyikének határegyenesével vagy nem.
Ha párhuzamos, akkor az a félsík, melynek határegyenesével párhuzamos, a 4. félsíkkal együtt máris lefedi a teljes síkot.
Ha nem párhuzamos, akkor van az első 3 félsík által fedetlenül hagyott résznek egy szögpontja, mely a negyedik félsík határegyeneséhez a legközelebb fekszik. Ez esetben a 4. félsík azzal a két félsíkkal együtt, melyeknek határegyenesei a legközelebb fekvő szögpontban metszik egymást, nyilván teljesen lefedi a síkot (7. ábra).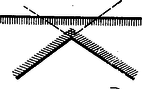

7. ábra

II. megoldás: Ha tételünk nem volna igaz, akkor a négy lefedő félsík közül rendre egy-egy félsíkot elhagyva fedetlenül marad minden egyes alkalommal legalább egy-egy pont, ami azt jelenti, hogy van a síkban négy olyan pont:

P_{1}

P_{2}

P_{3}

P_{4}

melyek mindegyike csak egyetlenegy félsíkkal van lefedve és ugyanakkor mindegyik félsik e 4 pont közül egy és csakis egy pontot fed le. Be fogjuk bizonyítani, hogy ilyen négy pont nem létezik.

Segédtétel: E négy pont közül három nem lehet egy egyenesen, mert az esetben a középső pont nem fedhető le egy félsíkkal úgy, hogy ugyanakkor a két szélső pont valamelyike ne kerüljön lefedésbe.
Marad tehát a 4 pont elhelyezésére a következő két eset:
a) Egy pont a másik három pont alkotta háromszögön belül van.
b) A négy pont egy konvex négyszöget alkot.
Az a) esetben jelöljük

P_{4}

-gyel a belső pontot és messe a

P_{3} P_{4}

egyenes a szemben fekvő

P_{1} P_{2}

oldalt

M

-ben 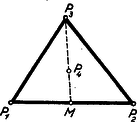(8. ábra).

8. ábra

Segédtételünk értelmében a

P_{4}

-et lefedő félsíknak le kell fednie vagy a

P_{3}

, vagy az

M

pontot is. Ugyancsak segédtételünkből következik, hogy minden

M

-et lefedő félsík

P_{1}

és

P_{2}

pontok valamelyikét lefedi. Így minden

P_{4}

-et lefedő félsík szükségképpen lefed még legalább egy pontot

P_{1}

P_{2}

és

P_{3}

közül.
b) esetben húzzuk meg a két átlót, ezek metszéspontja legyen

M

(9. ábr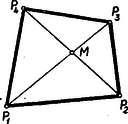a).

9. ábra

Segédtételünk értelmében minden

M

-et lefedő félsík fedi a

P_{1} P_{3}

átló egyik végpontját, és ugyanakkor a

P_{2} P_{4}

átló egyik végpontját is. Tehát minden

M

-et lefedő félsík legalább két

P

pontot fed le.
Ezzel tételünket bebizonyítottuk.

III. megoldás: Ha a 4 lefedő félsíkot két párban tekintjük, akkor feltehetjük, hogy egy-egy pár az I. megoldásban közölt (1) és (2) eset egyikét képviseli, mivel a (3) eset a (2)-re vezethető vissza.
Ha a két pár egyike a (2) esethez tartozik, akkor ‐ tekintve, hogy a két félsíkpár együtt lefedi az egész síkot ‐ az egyik pár által le nem fedett tartomány teljesen a síksáv egyik oldalán van és így a síksáv másik oldalát alkotó félsík elhagyható (lásd I. megoldás, 7. ábra).
Hátra van még az (1) ‐ (1) eset, vagyis amikor mindkét félsíkpár éket alkot. Itt ismét fennáll az, hogy ha két határegyenes (szögszár) párhuzamos, akkor e két határegyéneshez tartozó két félsík vagy lefedi a teljes síkot, vagy pedig e két félsík közül az egyik felesleges. Ha nincs párhuzamos határegyenes, akkor az egyik ék két félsíkjának elhúzásával (oly módon, hogy a mozgó félsíkok határegyenesei mindig párhuzamosak maradnak az eredeti határegyenesekkel) mindig elérhető az a helyzet, mikor a mozgó ék csúcspontja beleütközik a nyugvó ék egyik szárába (10/a ábra), vagy fordítva a mozgó ék egyik szára ütközik be a nyugvó ék csúcspontjába (10/b ábra).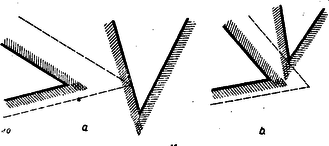

10. ábra

Mindkét esetben e csúcsponton átmenő 3 határegyeneshez tartozó 3 félsík már lefedi a teljes síkot, annál inkább áll fenn a lefedés a félsíkok visszatolása után. (Így bizonyította be a tételt a 2. díjnyertes, Kálmán Lajos.)

IV. megoldás: Ha egy egyenes véges számú félegyenessel teljesen le van fedve, akkor a félegyenesek két csoportba oszthatók aszerint, ahogy e félegyenesek a pozitív, illetőleg negatív irányban fedik le az egyenest a végtelenig. Mindegyik csoportba legalább egy félegyenes tartozik, mert véges számú egyirányú félegyenessel nem lehet egy egyenest teljesen lefedni. Ha az egyenest teljesen lefedő véges számú, pozitív irányú és negatív irányú félegyenesek közül kiválasztjuk azt az egy-egy félegyenest, mely az összes többi, vele egyirányú, félegyenest lefedi, akkor e 2 ellenkező irányú félegyenes már lefedi az egész egyenest. Tehát feladatunkban bármely félsík határegyenesét mindig 2 másik félsík már lefedi.
Most 3 esetet kell megkülönböztetni.
Ha a két lefedő félsík határegyenesei párhuzamosak egymással, akkor e két félsík már lefedi az egész síkot.
Ha a két lefedő félsík határegyeneseinek metszéspontja az első sík által lefedett tartományba esik, akkor ez a 3 félsík teljesen lefedi az egész síkot (11/a ábra).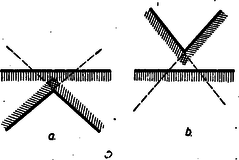

11. ábra

Végül, ha fenti metszéspont az első félsík által le nem fedett részbe esik, akkor az első félsík elhagyható (11/b ábra).
Megjegyzés: Ismeretes a koordináta geometriából, hogy

a x + b y + c = 0

egy egyenes egyenlete. Minden

x_{1}

y_{1}

számpárnak, melyre nézve

a x_{1} + b y_{1} + c = 0

, megfelel egy pont az egyenesen. Viszont, ha az

a x_{1} + b y_{1} + c > 0

, akkor

x_{1}

y_{1}

pont az

a x + b y + c = 0

egyenesnek azon az oldalán van, amelyen az origo, ha

c > 0

, és ellenkező oldalán, ha

c < 0

. Ez azt jelenti, hogy mindazon pontok összessége, melyek kielégítik az

a x + b y + c > 0

egyenlőtlenséget, egy félsík belső pontjai, mely félsíknak határegyenese az

a x + b y + c = 0

egyenes.
Ezek szerint most már bebizonyított tételünk így is fogalmazható:
Ha az alábbi négy egyenlőtlenségre

\begin{matrix} a_{1} x + b_{1} y + c_{1} > 0 \\ a_{2} x + b_{2} y + c_{2} > 0 \\ a_{3} x + b_{3} y + c_{3} > 0 \\ a_{4} x + b_{4} y + c_{4} > 0 \end{matrix}

fennáll, hogy bármilyen

x

y

számpár legalább egy egyenlőtlenséget kielégít, akkor mindig található a négy egyenlőtlenség között egy olyan, melyet elhagyva, az előbbi állítás a megmaradó három egyenlőtlenségre is fennáll. E tétel közvetlen bizonyítása nem volna egyszerű.