Kezdőlap


Feladat:	1951. évi Kürschák matematikaverseny 1. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Fáy Árpád , Kálmán Lajos , Seregély József , Szekerka Pál
Füzet:	1952/február, 4 - 6. oldal		PDF \| MathML
Témakör(ök):	Két pont távolsága, szakasz hosszúsága, Egyenesek egyenlete, Pitagorasz-tétel alkalmazásai, Körülírt kör, Trigonometrikus függvények, Háromszögek hasonlósága, Derékszögű háromszögek geometriája, Thalesz-kör, Középponti és kerületi szögek, Egyenlő szárú háromszögek geometriája, Négyzetek, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):	Feladatok: 1952/február: 1951. évi Kürschák matematikaverseny 1. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás: Helyezzük a négyzet $A$ csúcspontját derékszögű koordinátarendszer kezdőpontjába, az $A B$ oldalt a pozitív $Y$ tengelyre az $A D$ oldalt a pozitív $X$ tengelyre és tekintsük a négyzetoldalt egységnek (tehát $a = 1$ ), akkor feladatunk szerint az $A E$ egyenes egyenlete $y = 3 x$ és a $B F$ egyenes egyenle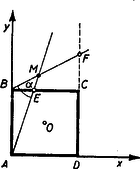te $y = 1 + \frac{x}{2}$ (1. ábra).

1. ábra

E két egyenes

M

metszéspontjának koordinátái:

\begin{matrix} x = 0, 4 és y = 1, 2 \end{matrix}

Számítsuk ki ezen

M

pont távolságának négyzetét a négyzet

O

(

0, 5

0, 5

) középpontjától

\begin{matrix} O M^{2} = {(0, 5 - 0, 4)}^{2} + {(0, 5 - 1, 2)}^{2} = 0, 1^{2} + 0, 7^{2} = 0, 01 + 0, 49 = \\ 0, 5 = 0, 5^{2} + 0, 5^{2} = O A^{2} . \end{matrix}

Tehát

O M = O A

. Ezzel tételünket bebizonyítottuk.

II. megoldás: Mivel a kerületi szögek tétele alapján a négyzet köré írt kör bármely pontjától a négyzet oldala

45^{\circ}

(illetve az egyik

135^{\circ}

) alatt látszik, azért tételünk bizonyítást nyert, ha kimutatjuk, hogy

A M B ∢ = α = 45^{\circ}

(1. ábra). A szögszárak iránytangensei az előbbiek szerint 3 és

\frac{1}{2}

, tehát

\begin{matrix} tg α = \frac{3 - \frac{1}{2}}{1 + 3 \cdot \frac{1}{2}} = 1, vagyis tényleg α = 45^{\circ} . \end{matrix}

III. megoldás: Jelöljük az

M

pont távolságát a

C D

négyzetoldaltól

M P = a

-val, és a

B C

négyzetoldaltól mért távolságát

M Q = b

-vel. Az

A E

egyenes messe a

C D

négyzetoldal meghosszabbítását

G

-ben (2. ábr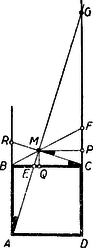a).

2. ábra

Nyilvánvaló, hogy

D G = 3

és mivel

D F

a feladat értelmében 1,5, ezért

F G = 1, 5

.
Az

M A B_{Δ} \sim M G F_{Δ}

és az oldalak aránya

\begin{matrix} A B : G F = 1 : 1, 5 = A M : M G . \end{matrix}

Ebből következik, hogy

A G : M G = 2, 5 : 1, 5 = A D : M P = 1 : a

, vagyis

\begin{matrix} a = \frac{1, 5}{2, 5} = 0, 6. \end{matrix}

Hasonlóképpen

B F C_{Δ} \sim B M Q_{Δ}

és így

\begin{matrix} M Q : F C = B M : B F = A M : A G = 1 : 2, 5. \end{matrix}

Ebből

M Q = b = \frac{F C}{2, 5} = \frac{0, 5}{2, 5} = 0, 2.

A befogók aránya az,

M P C

derékszögű háromszögben

(\frac{0, 6}{0, 2})

ugyanaz, mint az

A B E

derékszögű háromszögben, miből következik, hogy

P M C ∢ = B A E ∢

. Mivel pedig

P M ⊥ A B

, azért a másik szögszár

M C

⊥ A E

, vagyis

M C ⊥ M A

, ami azt jelenti, hogy az

M

pont rajta van az

A C

négyzetátló fölé, mint átmérő fölé rajzolt Thales-körön, amely Thales-kör egyszersmind a négyzet köré írt kör. (Az

M C

merőlegességére lehetett volna

\frac{b}{a} = - \frac{0, 2}{0, 6} = - \frac{1}{3}

iránytangensből is következtetni, de nem akartunk ebbe a megoldásba, sem trigonometriát, sem koordináta geometriát közvetlenül bevonni.)

IV. megoldás: Messe az

A E

egyenes a

C D

oldal meghosszabbítását ismét

G

-ben és a

C M

egyenes az

A B

oldal meghosszabbítását

R

-ben (2. ábra), akkor az előbbiek alapján

\begin{matrix} B R : B A = F C : F G = 0, 5 : 1, 5 = 1 : 3, \end{matrix}

amiből

B R = \frac{A B}{3} = \frac{B C}{3}

. Ebből következik, hogy

A B E_{Δ} \sim C B R_{Δ}

, vagyis

M A B ∢ = M C B ∢

. De ha két kerületi szög egyenlő és egy-egy száruknak metszéspontja

(B)

a körön van, akkor a másik két szár metszéspontja

(M)

is e körön van. (Ez az I. díjnyertes, Szekerka Pál bizonyítása.)

V. megoldás: Helyezzük egész ábránkat egy négyzetrácsra úgy, hogy

A B C D

négyzetünk csúcspontjai egy legkisebb rácsnégyzet csúcspontjaival essenek egybe.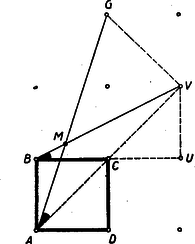

3. ábra

B C

oldalt meghosszabbítva az

U

rácspontig, az

A C

átlót pedig a

V

rácspontig (3. ábra), a keletkezett

B U V

derékszögű háromszög hasonló az

A V G

derékszögű háromszöghöz, mert mindkettőben a befogók aránya 2 : 1. Ebből következik, hogy az utóbbi háromszög

A

-nál fekvő szöge egyenlő az előbbi

B

-nél fekvő szögével, amiből viszont a kerületi szögek tétele alapján (hasonlóképpen mint a IV. megoldásban) következik, hogy

M

rajta van a négyzet köré írt körön.

VI. megoldás: Húzzuk meg az

A U

egyenest (4. ábra), ez nyilván párhuzamos a

B M

egyenessel, mert mindkettő iránytangense

\frac{1}{2}

. Az

A U G

háromszög nyilván derékszögű egyenlő szárú és így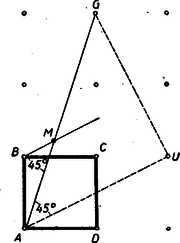

A ∢

-e

45^{\circ}

-os.

4. ábra

Ennek váltószöge, az

A M B ∢

tehát szintén

45^{\circ}

-os, amivel tételünket bebizonyítottuk. (L. a II. megoldást.)