Kezdőlap


Feladat:	1950. évi Kürschák matematikaverseny 3. feladata	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Wellisch Tibor
Füzet:	1951/május, 8 - 11. oldal		PDF \| MathML
Témakör(ök):	Oszthatóság, Természetes számok, Négyzetrács geometriája, Háromszögek nevezetes tételei, Kombinatorikai leszámolási problémák, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):	Feladatok: 1951/május: 1950. évi Kürschák matematikaverseny 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A feladat megoldása tulajdonképpen nem kíván különösebb ötleteket, csak kitartóan végig kell próbálni az összes lehetőségeket.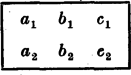
Hogy rövidebben fejezhessük ki magunkat, néhány rövid jelölést fogunk használni. Amit az együtthatókról tudunk, egy keretben fogjuk feltüntetni:

Ha egy együtthatóról azt tudjuk, hogy páros egészszám, akkor a helyébe egy

2

-est írunk, ha azt tudjuk, hogy páratlan egészszám, akkor

1

-est; ha pedig az derül ki, hogy két együttható összege páros egészszám, akkor ezek helyét egy

\circ - \circ

jellel kötjük össze. Az üresen hagyott helyek azt jelentik, hogy a megfelelő együtthatókról még nem derült ki semmi.

(x, y) = (a, b)

-vel azt jelöljük, hogy

x

helyébe

a

-t,

y

helyébe

b

-t helyettesítünk.

I. megoldás:

1^{\circ}

(x, y) = (0,0)

helyettesítéssel, azt kapjuk, hogy

c_{1}

és

c_{2}

közül valamelyik páros egészszám. Feltehetjük, hogy

c_{1}

ez:

2^{\circ}

. Helyettesítsünk

(x, y) = (1,0)

-t. Ha

a_{1} + c_{1}

páros,

a_{1}

is páros, ha nem akkor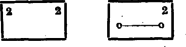

a_{2} + c_{2}

páros:

3^{\circ}

(x, y) = (- 1,0)

helyettesítésnél az első esetben biztos páros az első kifejezés, a másodikban mivel

- a_{1} + c_{1}

nem lehet páros (akkor

a_{1} + c_{1}

is az volna), tehát

- a_{2} + c_{2}

kell, hogy páros legyen. Ez csak úgy lehet, ha vagy

a_{2}

c_{2}

is páros egészszám, vagy mindkettő páratlan:

4^{\circ}

(x, y) = (0,1)

. Az első esetben, ha

b_{1} + c_{1}

páros

b_{1}

is az, ha nem akkor

b_{2} + c_{2}

páros. A másodikban ha

b_{1} + c_{1}

páros

b_{1}

is az, ha nem akkor

b_{2} + c_{2}

páros, de akkor

b_{2}

páros egészszám kell legyen. A harmadikban ha

b_{1} + c_{1}

páros, akkor

b_{1}

-nek páros egésznek kell lennie. Ha nem, akkor

b_{2} + c_{2}

páros, de akkor

b_{2}

páratlan egészszám:

1

. és

4

. esetben bármely egész

(x, y)

-ra az egyik kifejezés értéke páros lesz. Ezeket az eseteket nem is vizsgáljuk tovább.

5^{\circ}

. Legyen

(x, y) = (0, - 1)

2

.-ben

- b_{1} + c_{1}

nem lehet páros, mert akkor

b_{1}

és

b_{1} + c_{1}

is páros lenne. Így

- b_{2} + c_{2}

páros, tehát vagy mindkettő páros egészszám, vagy mindkettő páratlan. Az első lehetőség csak a két kifejezés sorrendjében különbözik a

3

. esettől, így nem tárgyaljuk külön.

3

.-ban és

5

.-ben az első,

6

.-ban a második kifejezés biztosan páros:

6^{\circ}

. Legyen

(x, y) = (1,1)

1

.-ben

a_{1} + b_{1} + c_{1}

nem lehet páros, mert feltettük (

4

.-nél), hogy

b_{1} + c_{1}

nem páros, tehát kell, hogy

a_{2} + b_{2} + c_{2}

legyen páros.

b_{2} + c_{2}

páros, így

a_{2}

is páros.

2

.-ben hasonlóan kell, hogy

a_{2} + b_{2} + c_{2}

legyen páros s így

b_{2}

páros egészszám, amivel viszont lényegében a már elintézett esetre jutunk.

3

.-ban sem lehet

a_{1} + b_{1} + c_{1}

páros, így

a_{2} + b_{2} + c_{2}

az, amiből következik, hogy

b_{2}

páros egésszám.

4

.-ben

a_{2} + b_{2} + c_{2}

páratlan egészszám, tehát biztosan

a_{1} + b_{1} + c_{1}

páros, tehát

a_{1} + b_{1}

is páros.

a_{1}

-ről viszont

2

.-ben feltettük, hogy nem páros (t. i. azzal, hogy

a_{1} + c_{1}

nem p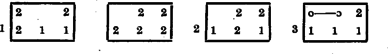áros).

A bizonyítandó állítást ezzel már meg is kaptuk, hisz itt minden esetben a második kifejezés együtthatói egészszámok. A további helyettesítések csak a táblázatok teljes kitöltéséért történnek:

7^{\circ}

. Legyen

(x, y) = (2,0)

1

.-ben

2 a_{1} + c_{1}

biztos páros, így nem tudunk meg újabbat.

2

.-ben az első kifejezésnek kell párosnak lennie, tehát

2 a_{1} + c_{1}

-nek, s így

2 a_{1}

-nek is.

a_{1}

tehát egész. Új eredményt csak akkor kapunk, ha

a_{1}

páratlan.

3

.-ban szintén az első kifejezés s így

2 a_{1}

külön is páros,

a_{1}

viszont nem az, így

a_{1}

és vele együtt

b_{1}

is páratlan egészszám:

8^{\circ}

. Az első esetben

b_{1}

megismerésére helyettesítsünk

(x, y) = (0,2)

-t.

2 b_{2} + c_{2}

páratlan, így

2 b_{1} + c_{1}

, tehát

2 b_{1}

is páros,

b_{1}

tehát egészszám. Ha páros, újat nem kapunk, tehát újabb lehetőség csak az, ha

b_{1}

páratlan.

Így a következő öt eset lehetséges:

Az első kettőben csak a két elsőfokú kifejezés sorrendje, az utolsó kettőben pedig csak

x

és

y

szerepe van felcserélve. Így ezek nem lényegesen különböző esetek. Az első két esetben minden egész

x

y

párra ugyanaz a kifejezés páros. A harmadikban, ha

x

y

is páros, vagy mindkettő páratlan, akkor az első, ha egyik páros, másik páratlan, akkor a második kifejezés lesz páros. A negyedik esetben páros

x

-re, az ötödikben páros

y

-ra az első kifejezés lesz páros,

y

illetőleg

x

párosságától függetlenül; páratlan

x

-re ill.

y

-ra viszont, a második.
Ez a megoldás nehézségekbe nem ütközik, de fáradságos. Ilyenkor igyekszünk a próbálgatásokat lehetőleg ügyesen elrendezni, hogy kevés esetet szétválasztva gyorsan és áttekinthető módon juthassunk e] a kívánt eredményhez.

II. megoldás: Tekintsük az

(1,0)

(0,0)

és

(- 1,0)

helyettesítéseket. A három helyettesítés közül legalább valamelyik kettőre ugyanannak a kifejezésnek kell páros egészszámot adnia, mert összesen két kifejezésünk van. Bármelyik két helyettesítésre is lesz e kifejezés páros, biztos, hogy benne

a

és

c

egészszámok.
Ugyanezzel az okoskodással adódik a

(0,1)

(0,0)

(0, - 1)

helyettesítések segítségével, hogy valamelyik kifejezésben

b

és

c

egészszám.
Ha mindkétszer ugyanarról a kifejezésről van szó, akkor

a

b

c

is egészszám. Ha

a

és

c

az egyik kifejezésben bizonyul egésznek,

b

és

c

viszont a másikban, akkor

(1,1)

behelyettesítésével látjuk, hogy valamelyik kifejezésben

a + b + c

is egész.
Mivel két együtthatóról már tudjuk, hogy külön-külön egészszám, így következik, hogy a harmadiknak külön is egésznek kell lennie, így minden esetben valamelyik kifejezésben

a

b

c

is, egészszám.

III. megoldás: Tekintsünk a számsíkon

5

pontot: a

(0,1)

(0, - 1)

(1,0)

(- 1,0)

és

(0,0)

pontokat. Ha

(x, y)

helyébe ezt az öt értéket helyettesítjük, valamelyik kifejezés mindegyik esetben páros egész értéket ad, így bizonyos, hogy az öt helyettesítés közül háromra ugyanaz a kifejezés lesz páros. Jelöljük együtthatóit index nélkül

a

b

c

-vel. Legyen a három helyettesítés

(x_{1}, y_{1})

(x_{2}, y_{2})

és

(x_{3}, y_{3})

. Ez esetben

a x_{1} + b y_{1} + c = 2 A

a x_{2} + b y_{2} + c = 2 B

a x_{3} + b y_{3} + c = 2 C

, ahol

A

B

és

C

egészszámok.
Szorozzuk meg az első egyenletet

(y_{2} - y_{3})

-mal, a másodikat

(y_{3} - y_{1})

-gyel, a harmadikat

(y_{1} - y_{2})

-vel és adjuk őket össze. Ekkor

b

és

c

szorzója éppen

0

lesz. A jobboldalon pedig újra páros szám keletkezik. Jelöljük

2 D

-vel:

\begin{matrix} a [x_{1} (y_{2} - y_{3}) + x_{2} (y_{3} - y_{1}) + x_{3} (y_{1} - y_{2})] = 2 D . \end{matrix}

Ha a számpárokat pontok koordinátáinak fogjuk fel, akkor a szorzója éppen a három pont által alkotott háromszög kétszeres területe, ezt

2 T

-vel jelölve, egyenletünk ilyen alakú lesz:

a \cdot 2 T = 2 D

. A fenti egyenleteket sorra

(x_{2} - x_{3})

-mal,

(x_{3} - x_{1})

-gyel,

(x_{1} - x_{2})

-vel szorozva és összeadva hasonlóan nyerjük, hogy

b \cdot 2 T = 2 E

, ahol

E

egészszám. Nézzük meg, most az öt számpárt ábrázoló pontokat. Ezek közül minden módon kiválasztva hármat vagy

1

, vagy

\frac{1}{2}

területű háromszöget kapunk, vagy egy egyenesbe esik a három pont. Tehát

2 T

értéke

2

1

vagy

0

. Első két esetben

a = \frac{2 D}{2 T}

és

b = \frac{2 E}{2 T}

s így velük együtt

c = 2 A - a x_{1} - b y_{1}

is egészszámok. Ha a három pont egy egyenesre esik és a másik két pontnak megfelelő két helyettesítésre a másik kifejezés ad páros értéket, akkor végezzük el még az

(1,1)

helyettesítést. Ha erre ismét az első kifejezés lesz páros, akkor a most hozzávett pont és a

3

egy egyenesen sorakozó pont közül a két szélső alkot egy

1

területű háromszöget, ha pedig itt a második kifejezés értéke páros, akkor ez a pont és az ötből kimaradó két pont alkot egy ugyanilyen háromszöget. Ezek valamelyikével ismételhetjük tehát meg a fenti gondolatmenetet. Valamelyik kifejezésnek tehát mindegyik esetben mindhárom együtthatója egész.