Feladat: 1950. évi Kürschák matematikaverseny 2. feladata Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Korányi Ádám ,  Szekerka Pál ,  Zergényi Erzsébet 
Füzet: 1951/május, 5 - 8. oldal  PDF  |  MathML 
Témakör(ök): Tengelyes tükrözés, Középpontos és egyéb hasonlósági transzformációk, Egyenlő szárú háromszögek geometriája, Kör geometriája, Hatványvonal, hatványpont, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):Feladatok: 1951/május: 1950. évi Kürschák matematikaverseny 2. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

E feladat megoldói közül egy kivételével, senki nem látta világosan, hogy három különböző esetet kell megvizsgálni: midőn a három kör kivülről érinti egymást, midőn k1 és k2 a k3 kör belsejében van és midőn k3 az egyik kört belülről, a másikat kívülről érinti. A továbbiakban hol egyik, hol másik, helyzetben tárgyaljuk a bizonyítást utalva a többi esetekben fellépő módosításra. Használni fogjuk a következő jelöléseket: a körök középpontja O1, O2, O3; k2 és k3, k3 és k1, k1 és k2 érintési pontja rendre A, B, C, az AC és BC egyenesek a k3 kört a D és E pontban metszik. (Ábra a köv. oldalon.)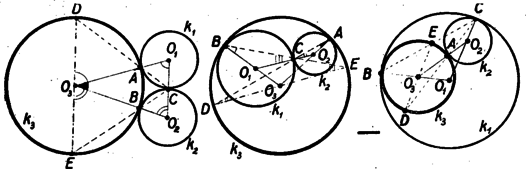

 
 

I. megoldás: Vizsgáljunk kivülről érintkező köröket. Legyenek az O1O2O3 háromszög szögei rendre α, β és γ. AO2CΔ és AO3DΔ egyenlőszárú és A-nál lévő szögeik egyenlők, mert csúcsszögek. Ha két egyenlőszárú háromszögben az alapnál fekvő egy-egy szög egyenlő, akkor az összes szögek egyenlők. Így AO3D∢=AO2C∢=β. Ugyanúgy következik a BO1C és BO3E egyenlőszárú háromszögekből, hogy BO3E∢=α. Így a DO3E∢ egy α, egy β és egy γ nagyságú szögből tevődik össze, tehát 180∘-os, vagyis a D, O3 és E pont egy egyenesen, a k3 kör egy átmérőjén fekszik.
Ha a k3 kör tartalmazza k1-et és k2-t, akkor a megoldásban szereplő háromszögpároknak az A ill. B csúcsnál fekvő szögei közösek és az O1-nél O2-nél illetve O3-nál fekvő külső szögek egyenlőségét használva fel okoskodhatunk az előbbi módon. Ha k3 a k1 kör belsejében és a k2 körön kívül van, akkor az első háromszögpárral az első esetnél, a másodikkal pedig a második esetnél elmondott módon okoskodunk és ismét arra az eredményre jutunk, hogy a DO3 és EO3 szárak között egy háromszög három szöge, vagyis éppen 180∘ fekszik.
 
II. megoldás: Legyen k1 és k2 a k3 kör belsejében. Elég megmutatnunk, hogy DO3‖EO3, mert a két egyenes egy pontja közös, tehát ez esetben egymás meghosszabbításába kell esniök.
Ismét nézzük az AO2C és AO3D egyenlőszárú háromszögeket. A-nál levő szögük közös, tehát az alapon fekvő másik szögek is egyenlők: ACO2∢=ADO3∢. E szögek egy szára közös, s így megfelelő szögek, másik száruk is párhuzamos: CO2‖DO3. Ugyanígy kapjuk, hogy CO1‖EO3. De O1, C és O2 egy egyenesen vannak, a két érintkező kör centrálisán, így DO3 és EO3 egymással is párhuzamosak, amiből következik a bizonyítandó állítás.
Ha kívülről érintkező köröket vizsgálunk, akkor a háromszögpároknak egy-egy szöge csúcsszöget alkot, az alapjukon levő második szögek ez esetben váltószögek lesznek, tehát száraik ismét párhuzamosak. A harmadik esetben ismét az egyik háromszög párra úgy okoskodunk, mint az első, a másodikra úgy, mint a második esetben.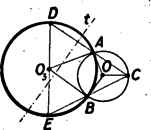
 
III. megoldás: Átfogalmazzuk a feladatot. Jelöljük O-val a három kör hatványpontját. (A közös érintők közös metszéspontját). Az O-ból a körökhöz húzott érintődarabok egyenlők OA=OB=OC. Így O köré olyan k kört lehet írni, mely átmegy az A, B, C pontokon, és merőlegesen metszi mindhárom kört, mivel az érintő merőleges a sugárra. A feladat tehát helyettesíthető a következővel: az egymást merőlegesen metsző k és k3 körök A és B metszéspontját a k kör tetszőleges C pontjából vetítjük. Bizonyítandó, hogy az AC és BC egyenesek második metszéspontja k3-mal, D és E átellenes pontok. Azt fogjuk megmutatni, hogy DO3 és EO3 ugyanarra az egyenesre merőleges. Ilyen egyenes CO. Tükrözzük ugyanis az ábrát egy CD-re merőleges t tengely körül.
 
 

Ha egy kört egy húrjának felezőmerőlegesére tükrözünk, akkor a húr végpontjához húzott sugarak egymásba mennek át. Ha nem a felezőpontban húzzuk a merőleges tengelyt, ezek az egyenesek akkor is egymással párhuzamos helyzetekbe mennek át. Így a k kört nézve CO tükörképe t-re párhuzamos lesz OA-val. k3-at nézve O3D képe párhuzamos lesz O3A-val. De a két kör merőlegesen metszi egymást, ami azt jelenti, hogy a metszésponthoz húzott körsugarak merőlegesek egymásra: OA⊥O3A. Ekkor azonban OC⊥O3D -re, mert a tükörképeik is merőlegesek egymásra. Ugyanígy következik egy CE egyenesre merőleges tengelyre tükrözve, hogy OC⊥O3E. Mivel az O3D és O2E egyenesek ugyanarra az egyenesre merőlegesek, így párhuzamosak egymással és miután az O3 pontjuk közös, következik, hogy D, O3 és E egy egyenesen feküsznek, k3 egy átmérőjén.
Ennél az átfogalmazásnál a kezdetben említett három eset abban különbözik, hogy C a k kör különböző részeire esik, a bizonyítás azonban ettől függetlenül minden esetben érvényes.
A feladat átfogalmazása egy általánosítást is kínál, melyet a 299. feladatban tűzünk ki (40 old.).
 
IV. megoldás. A bizonyítandó állítás következik abból is, hogy ha megmutatjuk, hogy a D-ben és E-ben húzott érintők párhuzamosak.
Nézzünk először két kört, k és k3 érintik egymást a B pontban. Középpontjuk legyen O és O3. Egy B-n átmenő egyenes k-t C-ben, k3-at E-ben metszi OBC∢=O3BE∢. (Belülről érintkező köröknél egybeesik a két szög, külső érintkezésnél csúcsszögek).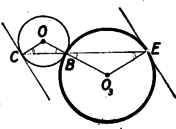
 
 

Mivel BOCΔ és BO3EΔ egyenlőszárú, következik, hogy OCB∢=O3EB∢. B, C és E egy egyenesbe esnek, így következik, hogy OC‖O3E. (Belső érintkezésnél megfelelő szögek szárai, külső érintkezésnél váltószögekéi.) De ekkor a C-ben és E-ben húzott érintők, melyek ezekre a sugarakra merőlegesek, szintén párhuzámosak. Ezt a meggondolást a k2 és k3 körökre alkalmazva ugyanúgy következik, hogy a C-ben és D-ben húzott érintők is párhuzamosak.
Még rövidebben mondhattuk volna el a bizonyítást, ha hivatkoztunk volna arra, hogy érintkező köröknek hasonlósági pontja az érintkezési pont, s azokban a pontokban, melyek ennél a hasonlóságnál egymásnak felelnek meg, az érintők párhuzamosak (Az előzőkben ennek az állításnak egy bizonyítását mondtuk el.) Hasonló tétel igaz térben is; érintkező gömbökre, érintők helyett érintő síkokkal, és felhasználható a feladat térbeli megfelelőjének bizonyítására, melyet a 305. feladatban tűzünk ki (41. old.).