Feladat: 1949. évi Kürschák matematikaverseny 3. feladata Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Bognár János ,  Czipszer János ,  Korányi Ádám 
Füzet: 1950/március, 63 - 65. oldal  PDF  |  MathML 
Témakör(ök): Természetes számok, Négyzetrács geometriája, Oszthatóság, Trapézok, Téglalapok, Négyzetek, Kombinatorikai leszámolási problémák, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):Feladatok: 1950/március: 1949. évi Kürschák matematikaverseny 3. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

I. megoldás. Azok az [egynél nagyobb] számok, amelyek maguk páratlanok, vagy páratlan osztójuk van, felírhatók egymásután következő számok összegeként. A többi ‐ vagyis 2 hatványai ‐ pedig nem.
A (2k+1)n szám, amelynek van páratlan osztója, felírható az n-k-tól n+k-ig terjedő számok összegeként. Ha itt k>n és így negatív számmal kezdődne a sor, a negatív tagokat és a velük abszolút értékben megegyező pozitív tagokat elhagyva kaphatunk természetes számokból álló sort. [A maradó sor legalább két számból áll, mert az eredeti számsor páratlan számú tagbál álló és középen a pozitív n szám áll. Páratlan az elhagyott tagok száma is, mert ugyanannyi negatív tagot hagytunk el, mint pozitívot és még a 0-át. Mivel az utóbbi számok kevesebben vannak, mint az előbbiek és pedig páros számmal, tehát legalább 2-vel, így legalább két pozitív tag marad meg.]
Ha 2 hatványait fel lehet írni egymásután következő számok összegeként, feltétlenül páros számú tag összege lenne, mert a számtani haladvány összege osztható tagjainak számával, [ha ez páratlan szám], a mi számunknak pedig nincs páratlan osztója. Ha pedig a tagok száma páros, akkor az első és utolsó tag közül az egyik páros, a másik páratlan. Összegük tehát páratlan. A haladvány összege pedig osztható első és utolsó tagjának összegével [ha ez páratlan szám]. Tehát így azt kaptuk, hogy a számnak van páratlan osztója. Az a feltevésünk tehát, hogy 2 valamelyik hatványát fel lehet írni egymásután következő számok összegeként ellentmondásra vezet.

 

Korányi Ádám.

 

II. megoldás. Ha egy N szám megfelel a feladat feltételeinek, akkor ilyen alakú:
N=a+(a+1)+...+(a+n-1)=n(2a+n-1)2,
azaz
2N=n(2a+n-1),és ittn<2a+n-1.

Legyen N most egy tetszőleges pozitív egész szám és kétszenesének egy tényezőkre bontása 2N=p⋅q, jelentse p a kisebbik tényezőt. Milyen legyen ez a felbontás, hogy a fenti alakban lehessen íni? Mindenesetre kell, hogy p=n, q=2a+n-1 legyen, azaz
n=p,a=q-p+12
ebben az esetben. Ahhoz, hogy itt a is egész szám legyen, p és q közül az egyiknek párosnak, a másiknak páratlannak kell lennie. Ha ez teljesül, akkor a-tól kezdve n egymásutáni szám összege a fentiek szerint N-nel egyenlő.
2N-nek ilyen tényezőkre bontása mindig van ha van páratlan osztója, tehát ha N páratlan, vagy van páratlan osztója. 2 hatványai tehát nem írhatók egymásutáni természetes számok összegeként, minden más szám viszont igen.
 

III. megoldás. Geometriailag könnyen szemléltethetjük egymástitáni természetes számok összegét pl. kockás papíron. Hogy könnyen tudjuk magunkat kifejezni, nevezzük a metszéspontokat rácspontoknak, Egy-egy számot egy vonalon megjelölt egymásutáni rácspontokkal ábrázolhatunk, az egymásutáni számokat pedig szomszédos egyeneseken rajzoljuk meg. Így egy ,,lépcsős trapézt'' jelöltünk ki, mely a határán és belsejében annyi rácspontot tartalmaz, mint a természetes számok összege.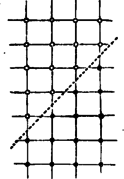
 
 

Illesszünk mellé megfordítva még egy ugyanilyen lépcsős trapézt. Ekkor téglalapot kapunk, mely kétszer annyi rácspontot tartalmaz, mint egy lépcsős trapéz. A két lépcsős trapézt az oldalakkal 45∘-os szöget bezáró egyenes választja el, mely átmegy a téglalap középpontján.
Ha már most van egy N egész számunk, úgy próbálhatunk N számú rácspontból lépcsős trapézt csinálni, hogy először 2N rácspontot tartalmazó téglalapot rajzolunk, azután ezt a középpontján át húzott 45∘-os egyenessel kettévágjuk. Így mindig két lépcsős trapézt kapunk, ha az egyenes nem megy át rácsponton. Ez az egyenes pedig rácspontokon megy át, ha maga a téglalap középpontja is rácspont, vagyis ha a téglalap mindegyik oldalán van középső rácspont; de rácspontokon megy át akkor is, ha a téglalap középpontja egy kis négyzetnek is középpontja, vagyis ha a téglalap egyik oldalán sincs középső rácspont.
Az előbbi azt jelenti, hogy az oldalak mind páros számú rácspontból állnak, az utóbbi azt, hogy mind páratlan számúból.
Lépcsős trapéz tehát akkor szerkeszthető, ha tudunk 2N rácspontot tartalmazó téglalapot rajzolni, melynek egyik oldalpárja páratlan, a másik páros számú rácspontot tartalmaz, azaz ha 2N egy páros és egy páratlan szám szorzataként írható. Ebből ismét következik, hogy 2 hatványainak kivételével minden természetes szám felírható egymásután természetes számok összegeként.
A III. feladat kapcsán felmerülő további kérdések közül érdekes a válasz a következőre, melyet ki is tűzünk megoldásra.
187. Melyek azok a természetes számok, melyek felírhatók legalább 3 egymásutáni természetes szám összegeként?