Feladat: 1949. évi Kürschák matematikaverseny 2. feladata Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Czipszer János ,  Fried Ervin ,  Róna Péter 
Füzet: 1950/május, 105 - 109. oldal  PDF  |  MathML 
Témakör(ök): Egyenlő szárú háromszögek geometriája, Középponti és kerületi szögek, Tengelyes tükrözés, Középpontos és egyéb hasonlósági transzformációk, Alakzatok szimmetriái, Pont körre vonatkozó hatványa, Körsorok, Inverzió, Háromszögek hasonlósága, Körülírt kör, Trapézok, Húrnégyszögek, Szimmetrikus alakzatok, Kürschák József (korábban Eötvös Loránd)
Hivatkozás(ok):Feladatok: 1950/március: 1949. évi Kürschák matematikaverseny 2. feladata

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

E feladatnak több megoldását adjuk, majd a feladat általánosításával is foglalkozunk.

 

I. megoldás. Az egyenlőszárú háromszög csúcsát A-val, másik két szögpontját B-vel és C-vel jelöljük. A Q pont az AC száron, az R pont az AB száron van. A P pontnak a QR egyenesre vonatkozó tükörképét D jelöli.
 
 

Az A, B, C, D pontok egy körön vannak, ha
ABD∢=ACD∢.
Feladatunk megoldása ennek az egyenlőségnek igazolását jelenti. A szerkesztésből következik, hogy a QPCΔ és RBPΔ hasonló az ABCΔ-höz. Tehát ezek is egyenlőszárúak, azaz QC=QP és RB=RP. A tükrözés következménye, hogy QP=QD és RP=RD. Eredményeinket összevetve QC=QD és RB=RD, azaz a QCDΔ és RBDΔ egyenlőszárú. E két háromszög alapjánál fekvő szögek egyenlőségének bizonyítását tűztük ki éppen célunkul. Egyenlőszárú háromszögek alapjánál fekvő szögei egyenlők, ha csúcsuknál lévő szögeik egyenlők. A QCDΔ és RBDΔ csúcsánál fekvő szöge egyenlő, ha mellékszögeik egyenlők:
AQD∢=ARD∢.
E szögegyenlőséget kell tehát bizonyítanunk. Ezek a szögek az AQEΔ-ben és a DREΔ-ben szerepelnek. E háromszögeknek E-nél lévő szögei csúcsszögek s így egyenlők. A bizonyítandó egyenlőség tehát igaz, ha a háromszögek harmadik szögei egyenlők:
QAR∢=QDR∢.
E két szög viszont egyenlő, mert mindkettő egyenlő a QPR∢-gel: az egyik tükörképe, a másik az AQPR parallelogrammában vele szemközti szög.
 

II. megoldás. Ki kell mutatnunk, hogy az ABCD négyszög húrnégyszög. Ehhez viszont elég azt belátni, hogy e négyszög szemközti szögeinek összege egyenlő, ábránk esetében: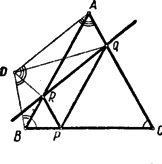
A∢+B∢=C∢+D∢.
Ugyanis e négy szög összege 360∘ és így ‐ ha az állított egyenlőség fennáll ‐ az ABCD négyszög szemközti szögeinek összege 180∘, tehát e négyszög húrnégyszög.
 
 

Az egyenlőszárú ABCΔ alapjánál fekvő szögei, ábránk egyíves szögei egyenlők. Az első megoldásból tudjuk, hogy az RBDΔ egyenlőszárú s így az ennek alapjánál fekvő szögek, ábránk kétíves szögei is egyenlők. Az AQRD négyszög szimmetrikus trapéz ugyanis átlói egyenlők: AR=QD (mindkettő egyenlő a QP távolsággal, egyrészt az AQPR paralelogramma szemközti oldalaiként, másrészt a tükrözés folytán), és két szemközti oldala egyenlő (az előbbi indokolás szerint mindkettő egyenlő az RP távolsággal). Az AQRD szimmetrikus trapéz egyik párhuzamos oldalánál fekvő szögei, ábránk három íves szögei tehát egyenlők.
Az állított szögegyenlőség mindkét oldala egy-egy egyíves, kétíves és háromíves szög összege. Ezért ez az egyenlőség valóban fennáll.
 

III. megoldás. Az első megoldásnál már beláttuk, hogy QC=QP=QD és RB=RP=RD. Tehát a C, P, D pontokon áthaladó kör középpontja Q, a B, P, D pontokon áthaladó kör középpontja pedig 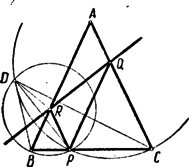R.
 
 

E körökre alkalmazzuk a kerületi és ugyanazon íven nyugvó középponti szögek tételét. E tétel szerint:
CDP∢=12CQP∢,PDB∢=12PRB∢.
A jobboldalakon szereplő szögek s a CAB∢-egyenlők, mert száraik párhuzamosak és egyirányúak. A baloldali szögek összege CDB∢. Egyenleteink összeadásából tehát
CDB∢=CAB∢
adódik s így A és D ugyanazon a B és C ponton áthaladó köríven van.
 

IV. megoldás. A második megoldásnál már beláttuk, hogy az AQRD négyszög szimmetrikus trapéz. Tehát a D pont az A pontnak tükörképe a QR távolság felező merőlegesére vonatkozólag.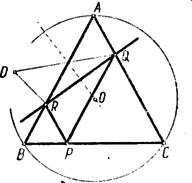
 
 

A kör kerületének egy pontját egy egyenesre tükrözve újból a kör kerületén lévő pontot kapunk, ha az egyenes áthalad a kör középpontján. Tehát azt kell belátnunk, hogy QR felezőmerőlegese áthalad az ABCΔ köré írt kör középpontján.
Két pont távolságának felező merőlegese akkor halad át egy kör középpontján, ha a két pont a kör középpontjától egyenlő távolságra van. Azt kell tehát igazolnunk, hogy Q és R az ABCΔ köré írt kör O középpontjától egyenlő távolságra van.
Az ABCΔ köré írt körben, a kör középpontja körül elforgatjuk a BA húrt, amíg a (vele egyenlő hosszú) AC húrt nem fedi. E forgatás az R pontot a Q pontba viszi, hiszen BR=AQ, mert a szerkesztés folytán mindkettő egyenlő a PR távolsággal. A kör középpontja körül való forgatással egymásba átvihető pontok a kör középpontjától egyenlő távolságra vannak. Tehát Q és R valóban egyenlő távolságra van az ABCΔ köré írt kör középpontjától.
 

V. megoldás. Rajzoljuk meg a harmadik megoldásban már szerepelt Q középpontú kört a C, P, D pontokon át s az R középpontú kört a B, P, D pontokon át.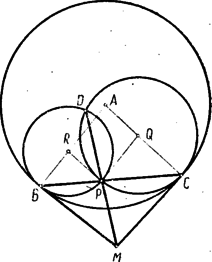
 
 

E körök C, ill. B pontban szerkesztett érintői merőlegesek az AC, ill. AB szárra. Tehát ezek az érintők egymást az ABCΔ tükörtengelyén lévő M pontban metszik és így MB=MC. Az M pontnak hatványa a szereplő két körre vonatkozólag MB, ill. MC négyzete. Ezek egyenlősége folytán M rajt van a két kör hatványvonalán. Ez a hatványvonal áthalad a körök metszéspontjain: a P ponton s ennek a körök középpontjait összekötő QR egyenesre vonatkozó tükörképén, a D ponton. Tehát M, P, D egy egyenesen helyezkednek el és a hatvány értelmezése szerint:
MP¯⋅MD¯=MB2¯=MC2¯.

Az előző számunkban a körsorokról írott második cikkben szerepelt az inverzió fogalma. E fogalom felhasználásával megállapításunkat úgy is szövegezhetjük, hogy a D pont a P pontnak az M körül MB=MC sugárral írt körre vonatkozó inverze. Minthogy P a BC egyenesen van, a D pont ennek az egyenesnek inverzén van rajt. Az idézett cikkből tudjuk, hogy egy egyenes inverze egy az inverzió pólusán áthaladó kör. Mivel a B és C pont önmagának inverze, a BC egyenes inverze az M, B, C pontokon áthaladó kör. Egy kör közös végpontú húrjainak másik végpontjában emelt merőlegesek a körön metszik egymást. Ezért az M, B, C pontokon áthaladó kör áthalad az MB és MC húrok végpontjaiban emelt merőlegesek A metszéspontján. Tehát a D pont rajt van az A, B, C pontokon áthaladó körön.
 

Megjegyzés az V megoldáshoz. Ábránkon az A pont körül AB=AC sugárral írt kört is megrajzoltuk. Ezt azért tettük, hogy a bizonyítottaknak érdekes átfogalmazását ugyanazzal az ábrával szemléltessük. Ha az ABCΔ-et érintetlenül hagyjuk, viszont a P pont helyzetét változtatjuk, akkor a korábban szerepelt körök s ezek P és D metszéspontjai is változtatják helyzetüket. E két kör sugarának összege az A körül írt kör sugara. A bizonyítottakat így a következőképpen fogalmazhatjuk:
Egy körbe két, belülről érintő kört írunk, melyek sugarának összege az első kör sugara. A beírt köröket érintési pontjuk változatlanul hagyása mellett változtatjuk: az egyik sugarát növeljük, a másikét ugyanannyival csökkentjük. E változtatás közben a két kör metszéspontjai közül az egyik az érintési pontokat összekötő szakaszon, a másik az érintési pontokon s az első kör középpontján áthaladó körön mozog.
 

Általánosítás. Ha a feladat állítását egyenlőszárú háromszög helyett általános háromszögre mondanók ki, helytelent állítanánk. Másként kell a feladatot megszövegezni, hogy tartalma általános háromszögre is helyes legyen. Ilyen átfogalmazás a következő:
Az ABC háromszög BC oldalán felvesszük a Ppontot. A PC szakasz felezőmerőlegese az AC oldalt Q pontban, a PB szakasz felezőmerőlegese az AB oldalt R pontban metszi. A P pontnak a QR egyenesre vonatkozó tükörképe az ABC háromszög köré írt körön van.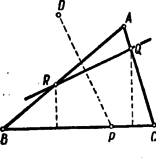
 
 

Az olvasó azonnal megállapíthatja, hogy egyenlőszárú háromszög esetében ez az általánosítás a versenyfeladat állítását adja. Érdekes megvizsgálni, hogy a versenyfeladatra adott bizonyításaink közül melyek használhatók fel az általánosítás bizonyítására is. Ennek eldöntését feladatként az olvasóra bízzuk (194. feladat).
Külön ki akarjuk emelni az ötödik megoldás átírásánál mutatkozó nehézséget. Ezt az átírást a következő feladat megoldása teszi lehetővé:
195. feladat. Az ABC háromszög BC oldalán E pontot veszünk fel. Megszerkesztjük az ABC háromszög köré írt kört, valamint az E ponton áthaladó s az AB egyenest B pontban, ill. az AC egyenest C pontban érintő kört. Bizonyítandó, hogy e három kör egy közös ponton halad át.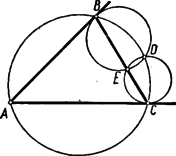
 
 

Megemlítjük, hogy e feladat állítása a már idézett cikkben szereplő Miquel-tétel határeseteként is felfogható. Ha ugyanis az ABC háromszög AC oldalán felvett F pont C-hez, az AB oldalon felvett G pont B-hez közeledik s a BC oldalon felvett E pont helyben marad, akkor az AFG kör az ABCΔ köré írt körré válik, a BEG és CEF körök pedig éppen a feladatunkban leírt helyzethez közelednek. E három kör, Miquel-tételének az idézett cikkben kiemelt speciális esete értelmében, egy ponton halad át. Ez áll a mondott határhelyzetre is. Éppen ennek határátmenet nélkül való bizonyítását bíztuk olvasóinkra.
 

196. feladat. A 195. feladat megoldásának birtokában már könnyű az ötödik megoldás bizonyítását az általánosítás bizonyításává átírni. Ennek kidolgozását is olvasóinkra bízzuk.
Leszögezzük, hogy e feladat megoldásával az eredeti versenyfeladatnak a közölt öthöz csatlakozó újabb megoldása adódik.