Kezdőlap


Feladat:	Gy.3131	Korcsoport: 14-15	Nehézségi fok: könnyű
Megoldó(k):	Babos Attila , Bákor Krisztina , Gulyás Zoltán , Gyenes Zoltán , Máthé András , Mészáros Albert , Mezei Gergely , Papp Dávid , Papp Eszter , Poronyi Gábor , Schmeiszer Kornél , Szép László , Tolvaj Nándor , Tóth Viktória , Velcsov Gabriella
Füzet:	1997/december, 536 - 537. oldal		PDF \| MathML
Témakör(ök):	Szabályos sokszögek geometriája, Sokszögek szimmetriái, Téglalapok, Középvonal, Gyakorlat
Hivatkozás(ok):	Feladatok: 1997/április: Gy.3131

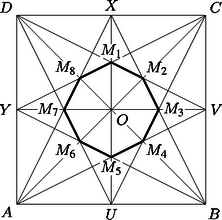
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a négyzet csúcsait $A$ , $B$ , $C$ , $D$ -vel, középpontját $O$ -val, oldalainak felezőpontját $X$ , $Y$ , $U$ , $V$ -vel, a nyolcszög csúcsait pedig az ábrán látható módon $M_{1}$ , $M_{2}$ , $...$ , $M_{8}$ -cal. A négyzet szimmetria tulajdonságai miatt az $U X$ , $V Y$ , $A C$ és $B D$ egyenesek 8 egybevágó háromszögre bontják a nyolcszöget. Megmutatjuk, hogy e háromszögek területe a négyzet területének $\frac{1}{48}$ része.

Legyen az egyszerűbb számolás kedvéért a négyzet oldala 12 egység. Ekkor

O V = 6

és

O M_{1} = \frac{1}{2} O X = 3

, mivel

Y V C D

téglalap, és ezért átlóinak

M_{1}

metszéspontja felezi az

O X

középvonalát. Tehát

T_{M_{1} O V} = \frac{1}{2} \cdot 6 \cdot 3 = 9

. Az

M_{3}

pont ugyanezért felezi az

O V

szakaszt, tehát

T_{O M_{2} M_{3}} = T_{V M_{2} M_{3}}

. Az

M_{1}

és

M_{3}

pontok pedig az

A C = O M_{2}

egyenesre szimmetrikusan helyezkednek el, ezért

T_{O M_{2} M_{3}} = T_{O M_{2} M_{1}}

. Így

\begin{matrix} 9 = T_{M_{1} O V} = T_{O M_{2} M_{1}} + T_{O M_{2} M_{3}} + T_{V M_{2} M_{3}} = 3 T_{O M_{2} M_{3}}, \end{matrix}

vagyis

T_{O M_{2} M_{3}} = 3

. A nyolcszöget 8 darab

O M_{2} M_{3}

-mal egybevágó háromszög alkotja, tehát a nyolcszög területe

8 \cdot 3 = 24

. Mivel a négyzet területe

12 \cdot 12 = 144

, azért a nyolcszög területe a négyzet területének egyhatoda. Ez az arány akármilyen négyzetre fennáll, speciálisan 10 egység oldalú négyzet esetén a nyolcszög területének mérőszáma

\frac{100}{6}

Velcsov Gabriella (Szeged, Radnóti M. Gimn., I. o.t.) dolgozata alapján