Kezdőlap


Feladat:	Gy.3130	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Juhász Ágnes , Lengyel Tímea , Máthé András , Naszódi Gergely , Papp Dávid
Füzet:	1997/december, 535 - 536. oldal		PDF \| MathML
Témakör(ök):	Beírt kör, Oldalfelező merőleges, Szögfelező egyenes, Egyenlő szárú háromszögek geometriája, Gyakorlat
Hivatkozás(ok):	Feladatok: 1997/április: Gy.3130

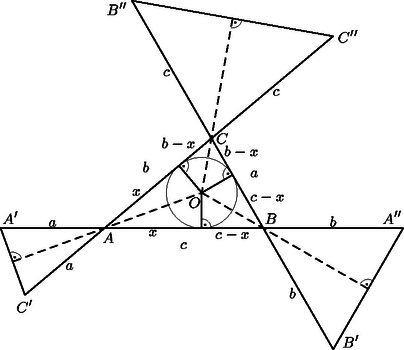
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük a háromszög csúcsait $A$ , $B$ , $C$ -vel; a csúcsokkal szemközti oldalakat rendre $a$ , $b$ , $c$ -vel; az oldalakra felmért szakaszok végpontjait ‐ az ábrán látható módon ‐ $A'$ , $C'$ , $B'$ , $A''$ , $C''$ , $B''$ -vel; az $A B C$ háromszög beírt körének középpontját $O$ -val; az $A$ -ból a beírt körhöz húzott érintőszakasz hosszát pedig $x$ -szel. Megmutatjuk, hogy az $A'$ , $B'$ , $C'$ , $A''$ , $B''$ , $C''$ pontok egy $O$ középpontú körön vannak.

A A' C'

B B' A''

és

C C'' B''

háromszögek egyenlő szárúak, ezért az alapjaik felezőmerőlegesei egybeesnek száraik szögfelezőivel. E szögfelezők viszont a csúcsszögek tulajdonságai miatt megegyeznek az

A B C

háromszög belső szögfelezőivel, s így átmennek

O

-n. Tudjuk, hogy egy körhöz egy külső pontból húzott két érintőszakasz egyenlő, ezért a

B

, illetve

C

pontból a beírt körhöz húzott érintőszakaszok hossza

c - x

, illetve

b - x

, így

B C = a = (c - x) + (b - x)

, amiből kapjuk, hogy

x = \frac{1}{2} (b + c - a)

. Tehát az

A'

-ből,

B'

-ből, illetve

C''

-ből a beírt körhöz húzott érintőszakaszok hossza rendre

a + x = b + (c - x) = c + (b - x) = \frac{1}{2} (a + b + c)

. Ezért az

A'

B'

C''

pontok

O

-tól való távolsága

\sqrt[]{{[\frac{1}{2} (a + b + c)]}^{2} + r^{2}}

, ahol

r

A B C

háromszög beírt körének sugara. Mivel már láttuk, hogy

O A' = O C'

O B' = O A''

és

O B'' = O C''

, azért ebből következik, hogy az

A'

A''

B'

B''

C'

és

C''

pontok egy ‐

O

középpontú ‐ körön vannak.

Juhász Ágnes (Miskolc, Avasi Gimn., I. o.t.) dolgozata alapján