Kezdőlap


Feladat:	Gy.3125	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Huszár Péter
Füzet:	1997/december, 534 - 535. oldal		PDF \| MathML
Témakör(ök):	Terület, felszín, Tetraéderek, Kocka, Pitagorasz-tétel alkalmazásai, Középvonal, Háromszögek egybevágósága, Gyakorlat
Hivatkozás(ok):	Feladatok: 1997/március: Gy.3125

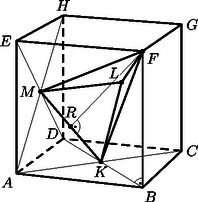
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A kocka bármelyik csúcsát kiválasztva, az általa és a rá nem illeszkedő lapok középpontjai által meghatározott tetraéderek egybevágóak, ezért elegendő egy ilyen tetraéder felszínét meghatározni. Jelöljük a kocka csúcsait az ábrán latható módon $A$ , $B$ , $C$ , $D$ , $E$ , $F$ , $G$ , $H$ -val; az $F$ -re nem illeszkedő lapok középpontjait $K$ , $L$ , $M$ -mel; $K M$ felezőpontját pedig $R$ -rel.

K L M F

tetraéder élei közül

K M = M L = L K = \frac{\sqrt[]{2}}{2} a

, mert ezek az

a \cdot \sqrt[]{2}

oldalú

A C H

háromszög középvonalai. Továbbá

K F = L F = M F

, mert mindegyik a kocka egyik lapjának középpontját köti össze a szemközti lap egyik csúcsával. E szakaszok hosszát Pitagorasz tétele segítségével számolhatjuk ki, pl.

K F^{2} = K B^{2} + B F^{2} = {(a \cdot \frac{\sqrt[]{2}}{2})}^{2} + a^{2} = \frac{3}{2} a^{2}

; így

K F = L F = M F = a \cdot \frac{\sqrt[]{6}}{2}

. A

K M F

L M F

és

L K F

háromszögek egybevágóak, mert megfelelő oldalaik megegyeznek. A

K M F

háromszög

K M

oldalához tartozó

F R

magasságának hossza ugyancsak Pitagorasz tétele szerint:

\begin{matrix} F R^{2} = F K^{2} - R K^{2} = F K^{2} - {(\frac{K M}{2})}^{2} = \frac{3}{2} a^{2} - \frac{1}{8} a^{2} = \frac{11}{8} a^{2}; \end{matrix}

ezért a háromszög területe

T_{K M F} = \frac{1}{2} K M \cdot F R = a^{2} \cdot \frac{\sqrt[]{11}}{8}

. A

K L M

szabályos háromszög területe

T_{K L M} = K M^{2} \cdot \frac{\sqrt[]{3}}{4} = a^{2} \cdot \frac{\sqrt[]{3}}{8}

. Tehát a tetraéder felszíne

\begin{matrix} A = T_{K L M} + 3 T_{K M F} = \frac{a^{2}}{8} (\sqrt[]{3} + 3 \sqrt[]{11}) \approx 1, 46 a^{2} . \end{matrix}

Huszár Péter (Révkomárom, Selye J. Gimn., II. o.t.) dolgozata alapján