Kezdőlap


Feladat:	Gy.3124	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Barát Anna , Dedinszky Zsófia , Gueth Krisztián , Gyenes Zoltán , Hangya Balázs , Helesfai Gábor , Huszár Péter , Katona Zsolt , Keszegh Balázs , Kósa Botond , Lengyel Tímea , Lippner Gábor , Máthé András , Naszódi Gergely , Páles Csaba , Papp Dávid , Szűcs Gábor , Terék Zsolt , Zábrádi Gergely
Füzet:	1997/december, 533 - 534. oldal		PDF \| MathML
Témakör(ök):	Háromszögek hasonlósága, Középvonal, Párhuzamos szelők tétele, Ceva-tétel, Gyakorlat
Hivatkozás(ok):	Feladatok: 1997/március: Gy.3124

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Mivel az $A_{1} C_{1}$ szakasz párhuzamos az $A C$ szakasszal, azért a $Q B_{1} A_{2}$ és a $B_{2} C_{1} A_{2}$ háromszögek hasonlóak, azaz $\frac{Q B_{1}}{B_{1} A_{2}} = \frac{B_{2} C_{1}}{C_{1} A_{2}}$ . Az $R B_{1} C_{2}$ és a $B_{2} A_{1} C_{2}$ háromszögek is hasonlóak, ezért $\frac{R B_{1}}{B_{2} A_{1}} = \frac{B_{1} C_{2}}{A_{1} C_{2}}$ . E két egyenletből $Q B_{1}$ -et és $R B_{1}$ -et kifejezve kapjuk, hogy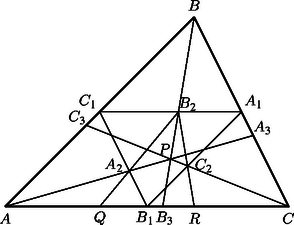

\begin{matrix} \frac{Q B_{1}}{R B_{1}} = \frac{B_{1} A_{2} \cdot B_{2} C_{1}}{C_{1} A_{2}} : \frac{B_{2} A_{1} \cdot B_{1} C_{2}}{A_{1} C_{2}} = \frac{B_{1} A_{2}}{A_{2} C_{1}} \cdot \frac{C_{1} B_{2}}{B_{2} A_{1}} \cdot \frac{A_{1} C_{2}}{C_{2} B_{1}} . \end{matrix}

Egy háromszög középvonalai párhuzamosak a háromszög megfelelő oldalaival, ezért ha

A_{3}

B_{3}

és

C_{3}

jelöli az

A P

B P

és

C P

egyeneseknek az

A B C

háromszög oldalaival alkotott metszéspontjait (ábra), akkor a párhuzamos szelők tétele alapján

\frac{B_{1} A_{2}}{A_{2} C_{1}} = \frac{C A_{3}}{A_{3} B}

\frac{C_{1} B_{2}}{B_{2} A_{1}} = \frac{A B_{3}}{B_{3} C}

és

\frac{A_{1} C_{2}}{C_{2} B_{1}} = \frac{B C_{3}}{C_{3} A}

. Vagyis

\begin{matrix} \frac{Q B_{1}}{R B_{1}} = \frac{C A_{3}}{A_{3} B} \cdot \frac{B C_{3}}{C_{3} A} \cdot \frac{A B_{3}}{B_{3} C} . \end{matrix}

A jobb oldalon álló szorzat értéke viszont Ceva tétele szerint (lásd pl. Horvay‐Reiman: Geometriai feladatok gyűjteménye I., 1263. feladat) 1, mert az

A A_{3}

B B_{3}

és

C C_{3}

egyenesek egy ponton,

P

-n mennek át.
Ez azt jelenti, hogy az

R B_{1}

és a

Q B_{1}

szakaszok hossza megegyezik, és éppen ezt akartuk bizonyítani.

Terék Zsolt (Fazekas M. Főv. Gyak. Gimn., III. o.t.)