Feladat: F.3157 Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Bérczi Gergely ,  Détári Dániel ,  Fejérvári Bence ,  Gyenes Zoltán ,  Hangya Balázs ,  Jeszenszky Gyula ,  Juhász András ,  Megyeri Csaba ,  Szűcs Gábor ,  Terék Zsolt ,  Varga Áron ,  Várkonyi Péter 
Füzet: 1997/szeptember, 351 - 352. oldal  PDF  |  MathML 
Témakör(ök): Háromszögek nevezetes tételei, Négyzetek, Terület, felszín, Háromszögek hasonlósága, Számtani-mértani egyenlőtlenségek, Szélsőérték-feladatok, Feladat
Hivatkozás(ok):Feladatok: 1997/január: F.3157

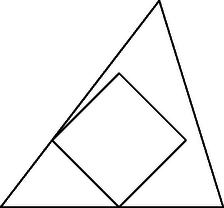
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A különböző alakú egységnyi területű háromszögek közül azokat kell megkeresnünk, amelyekbe maximális területű négyzet írható. Első lépésként megmutatjuk, hogy a maximális területű négyzet csúcsai szükségképpen a háromszöglemez határán lesznek. Ha a beírt négyzetnek legalább két csúcsa a háromszög belső pontja (1. ábra), akkor a háromszögnek van olyan csúcsa, amelyikből a nézetet nagyítva egy csúcs képe a kerületre kerül. Ezt ismételve elérhetjük, hogy három négyzetcsúcs a háromszög határán legyen, miközben a négyzet területe növekszik.
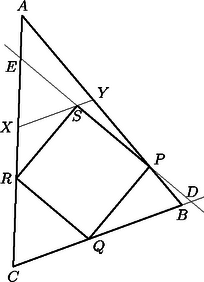
A 2. ábrán a négyzet három csúcsa a háromszög oldalaira illeszkedik. Az ábra jelöléseivel XY‖BC, és feltehetjük, hogy PB≤PY és CR≥RX. A PS egyenes a BC-t D-ben, az AC-t E-ben metszi. A PB≤PY feltevés miatt a PBD háromszög területe nem nagyobb, mint a PSY háromszögé. Ezért a CDE háromszög területe kisebb, mint az ABC háromszögé. Ha most a CDE háromszöget ‐ a négyzettel együtt ‐ úgy nagyítjuk, hogy területe egységnyi legyen, akkor a PQRS négyzet területe is növekedni fog.
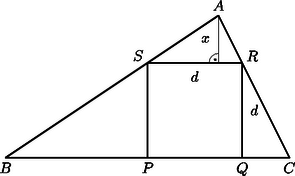
Az elmondottakból az látszik, hogy a maximális területű négyzet a 3. ábra szerint úgy helyezkedik el a háromszögben, hogy egyik oldala azon a háromszög-oldalon van, amelyiknek egyik csúcsában sincs tompaszög. Az ábra jelöléseivel az ASR és az ABC háromszögek hasonlóságából x:d=(x+d):BC, amiből BC=d(x+d)x. Így a háromszög területe 12⋅dx⋅(x+d)2, amit a számtani és mértani közép közötti egyenlőtlenséggel becsülve:
12⋅dx(d+x)2≥12⋅dx⋅(2dx)2=2d2.
Ez azt jelenti, hogy 2d2 akkor lesz a legnagyobb, ha annyi, mint a háromszög területe, és ez akkor lép fel, ha x=d. Ebben az esetben d2=12, és BC=x+d=2. Tehát a 2 alapú és 2 magasságú nem tompaszögű egységnyi területű háromszögekbe írható a legnagyobb négyzet.
 
Megjegyzés. A feladat megoldásában a beírt négyzet lefedett négyzet értelemben szerepelt. Szigorúbb értelemben beírt négyzet a 3. ábrán látható négyzet.