Feladat: N.111 Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Bérczi Gergely ,  Braun Gábor ,  Frenkel Péter ,  Gyenes Zoltán ,  Juhász András ,  Kiss Tamás ,  Kun Gábor ,  Kutalik Zoltán ,  Lippner Gábor ,  Mátrai Tamás ,  Megyeri Csaba ,  Pap Gyula ,  Prause István ,  Szabó Jácint ,  Terpai Tamás ,  Zubcsek Péter Pál 
Füzet: 1997/április, 224 - 225. oldal  PDF  |  MathML 
Témakör(ök): Gráfelmélet, Szélsőérték-feladatok differenciálszámítás nélkül, Nehéz feladat
Hivatkozás(ok):Feladatok: 1996/szeptember: N.111

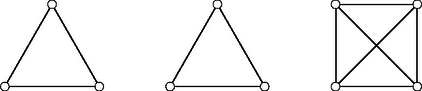
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelölje f(n) azt, hogy egy n csúcsú gráfban minimálisan hány élt kell behúzni ahhoz, hogy bármely 5 csúcs között legalább 2 él haladjon. A feladat f(10) meghatározása.
Azt állítjuk, hogy

f(n+1)≥n+1n-1f(n).
Tegyük fel, hogy egy n+1 pontú gráfban bármely 5 csúcs között legalább 2 él halad, és a gráf éleinek száma pontosan f(n+1). Hagyjuk el a legnagyobb fokszámú csúcsot és a belőle induló k darab élt; ezzel egy olyan n pontú, f(n+1)-k élű gráfot kapunk, amelyben továbbra is bármely 5 pont között legalább 2 él halad, következésképp legalább f(n) éle van. Az n+1 csúcsú gráfban a fokszámok összege az élszám kétszerese:
2f(n+1), ezért k≥2f(n+1)n+1. Összegezve az elmondottakat,
f(n)≤f(n+1)-k≤f(n+1)-2f(n+1)n+1,
amit átrendezve
f(n+1)≥n+1n-1f(n).

Ebből  f(5)=2  alapján  f(6)≥64f(5)=3;  f(7)≥75f(6)≥4,2,  azaz  f(7)≥5;
f(8)≥86f(7)≥6,66..., azaz f(8)≥7; f(9)≥97f(8)≥9; f(10)≥108f(9)≥11,25, azaz f(10)≥12.
Az ábrán látható gráfnak 10 csúcsa és 12 éle van, és megmutatjuk, hogy bármely 5 csúcsa között legalább 2 éle fut.
A gráf három komponensből áll: egy 4-pontú és két 3-pontú teljes gráfból. Ha kiválasztunk 5 csúcsot, ezek közül vagy lesz három, amelyek ugyanabba a komponensbe tartoznak, és akkor közöttük három él is fut, vagy pedig két komponensből választunk két-két pontot és a harmadikból egyet, ekkor pedig az egy komponensből választott pontpárok között fut két él.
A minimális élszám tehát 12.
 
Megjegyzés. A látott módszerrel bebizonyítható, hogy tetszőleges n-re a minimális élszám úgy érhető el, ha a gráf három olyan teljes gráf egyesítése, amelyekben a csúcsszám legfeljebb 1-gyel különbözik.
 Több dolgozat alapján