Feladat:	Gy.3092	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Balogh Attila ,  Benedek Csaba ,  Gyenes Zoltán ,  Hangya Balázs
Füzet:	1997/április, 215. oldal		PDF  |  MathML
Témakör(ök):	Kör geometriája, Gyakorlat
Hivatkozás(ok):	Feladatok: 1996/november: Gy.3092

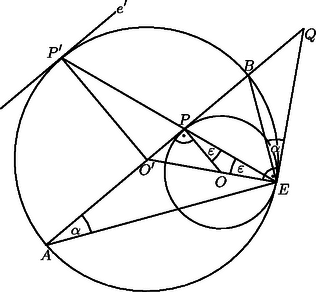
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Jelöljük a körök középpontjait az ábrán látható módon $O$-val és $O\text{'}$-vel. Messe a körök $E$-beli közös érintője az $AB$ egyenest $Q$-ban (ha a közös érintő párhuzamos $AB$-vel, akkor $EP$ merőleges $AB$-re, a feladat állítása nyilvánvaló). Feltehetjük, hogy $Q$ az $AB$ szakasz $B$-n túli meghosszabbításán van. Ekkor $BEQ\sphericalangle =BAE\sphericalangle =\alpha$, mert mindkettő a $BE$ ívhez tartozó kerületi szög. Nyilván $OPE\sphericalangle =OEP\sphericalangle =\epsilon$, (hiszen $OP=OE$), továbbá $OPA\sphericalangle =OEQ\sphericalangle ={90}^{\circ }$, mert a kör érintője merőleges az érintési pontba húzott sugárra. Az $AEP$ szöget az $AEP$ háromszög másik két szögével kifejezve kapjuk, hogy $\begin{array}{c}{\displaystyle AEP\sphericalangle ={180}^{\circ }-\left(PAE\sphericalangle +APE\sphericalangle \right)={180}^{\circ }-\left(\alpha +{90}^{\circ }+\epsilon \right)={90}^{\circ }-\alpha -\epsilon \mathrm{.}}\end{array}$ A $PEB$ szög pedig $\begin{array}{c}{\displaystyle PEB\sphericalangle =OEQ\sphericalangle -OEP\sphericalangle -BEQ\sphericalangle ={90}^{\circ }-\epsilon -\alpha \mathrm{.}}\end{array}$ Tehát $PE$ valóban felezi az $AEB$ szöget.   II. megoldás. Nagyítsuk $E$-ből középpontosan a kisebbik kört úgy, hogy képe a nagyobbik kör legyen. $P$ képe legyen $P\text{'}$, $AB$ képe $e\text{'}$, a további jelölések pedig egyezzenek meg az I. megoldásban használtakkal. Mivel $e\text{'}$ érintő, azért merőleges $O\text{'}P\text{'}$-re. Ekkor viszont $O\text{'}P\text{'}$ az $AB$ húrra is merőleges a nagy körben, mert