Kezdőlap


Feladat:	Gy.3091	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Babos Attila , Bajusz Csaba , Benedek Csaba , Bíró Anikó , Bíró Zsuzsanna , Bokros Krisztián , Bosznay Tamás , Bujdosó Attila , Csiszár Gábor , Davidovics Gábor , Gueth Krisztián , Gyenes Zoltán , Győri Nikolett , Keszegh Balázs , Klausz Ferenc , Kósa Botond , Kunszenti-Kovács Dávid , Lengyel Tímea , Lovrics Klára , Micskei Zoltán , Schlotter Ildikó , Somogyi Gábor , Szalontay Mihály , Szép László , Terpai Tamás , Tolvaj Nándor , Vaik István , Végh László
Füzet:	1997/május, 282 - 283. oldal		PDF \| MathML
Témakör(ök):	Háromszögek nevezetes tételei, Terület, felszín, Gyakorlat
Hivatkozás(ok):	Feladatok: 1996/november: Gy.3091

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.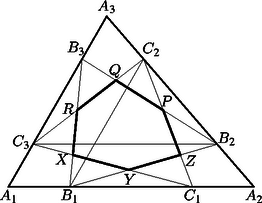

B_{1} B_{2} B_{3}

és a

C_{1} C_{2} C_{3}

háromszögek közös része egy hatszög. Jelöljük ennek csúcsait az ábrán látható módon

X

Y

Z

P

Q

R

-rel. A hatszög területét úgy fogjuk meghatározni, hogy a

C_{1} C_{2} C_{3}

háromszög területéből levonjuk az

Y Z C_{1}

P Q C_{2}

és

R X C_{3}

háromszögek területét. A számolás során azt az ismert tényt fogjuk felhasználni, hogy ha két háromszögnek közös az egyik szöge, akkor területük aránya megegyezik a közös szöget bezáró oldalak szorzatának arányával (

T = \frac{a b sin γ}{2}

miatt).
A

C_{i}

pontok definíciójából következik, hogy

A_{1} C_{1} = \frac{3}{4} A_{1} A_{2}

és

A_{1} C_{3} = \frac{1}{4} A_{1} A_{3}

, ezért

\begin{matrix} T_{A_{1} C_{1} C_{3}} = \frac{3}{4} \cdot \frac{1}{4} \cdot T_{A_{1} A_{2} A_{3}} . \end{matrix}

Ugyanígy kapjuk, hogy

\begin{matrix} T_{A_{2} C_{2} C_{1}} = T_{A_{3} C_{3} C_{2}} = \frac{3}{16} T_{A_{1} A_{2} A_{3}} . \end{matrix}

Ezért

T_{C_{1} C_{2} C_{3}} = T_{A_{1} A_{2} A_{3}} - (T_{A_{1} C_{1} C_{3}} + T_{A_{2} C_{2} C_{1}} + T_{A_{3} C_{3} C_{2}}) = \frac{7}{16} T_{A_{1} A_{2} A_{3}}

.
Mivel

B_{2}

és

C_{3}

negyedelőpontok, azért

B_{2} C_{3}

párhuzamos

A_{1} A_{2}

-vel, és

B_{2} C_{3} = \frac{3}{4} A_{1} A_{2}

. A

B_{2} C_{3} Y

és a

B_{1} C_{1} Y

háromszögek hasonlóak, mert szögeik megegyeznek. Ezért

\begin{matrix} \frac{C_{1} Y}{Y C_{3}} = \frac{C_{1} B_{1}}{C_{3} B_{2}} = \frac{\frac{1}{2} A_{1} A_{2}}{\frac{3}{4} A_{1} A_{2}} = \frac{2}{3}, \end{matrix}

tehát

C_{1} Y = \frac{2}{5} C_{1} C_{3}

. A

B_{1} C_{2}

és a

B_{2} C_{1}

szakaszok párhuzamosak

A_{1} A_{3}

-mal, és

B_{1} C_{2} = \frac{3}{4} A_{1} A_{3}

B_{2} C_{1} = \frac{1}{4} A_{1} A_{3}

. A

B_{1} C_{2} Z

és a

B_{2} C_{1} Z

háromszögek szögei egyenlők, ezért a két háromszögben a megfelelő oldalak aránya is egyenlő:

\begin{matrix} \frac{C_{1} Z}{Z C_{2}} = \frac{C_{1} B_{2}}{C_{2} B_{1}} = \frac{\frac{1}{4} A_{1} A_{3}}{\frac{3}{4} A_{1} A_{3}} = \frac{1}{3}, \end{matrix}

tehát

C_{1} Z = \frac{1}{4} C_{1} C_{2}

.

Vagyis

T_{C_{1} Y Z} = \frac{2}{5} \cdot \frac{1}{4} T_{C_{1} C_{3} C_{2}}

. Ugyanígy kapjuk, hogy

T_{C_{2} Q P} = T_{C_{3} X R} = \frac{1}{10} T_{C_{1} C_{2} C_{3}}

.
Tehát

\begin{matrix} T_{P Q R X Y Z} = T_{C_{1} C_{2} C_{3}} - (T_{C_{1} Y Z} + T_{C_{2} Q P} + T_{C_{3} X R}) = \frac{7}{10} T_{C_{1} C_{2} C_{3}} = \frac{7}{10} \cdot \frac{7}{16} T_{A_{1} A_{2} A_{3}} . \end{matrix}

Ezért a keresett arányszám

\frac{49}{160}

Bosznay Tamás (Bp., ELTE Apáczai Csere J. Gimn., II. o.t.) dolgozata alapján