Feladat:	Gy.3082	Korcsoport: 16-17	Nehézségi fok: könnyű
Megoldó(k):	Benedek Csaba ,  Hesz Gábor ,  Papp Dávid ,  Savanya Márta
Füzet:	1997/március, 156 - 158. oldal		PDF  |  MathML
Témakör(ök):	Derékszögű háromszögek geometriája, Szögfelező egyenes, Magasságvonal, Hossz, kerület, Pitagorasz-tétel alkalmazásai, Terület, felszín, Gyakorlat
Hivatkozás(ok):	Feladatok: 1996/október: Gy.3082

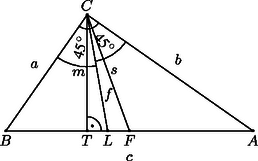
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Jelöljük a háromszög oldalait és csúcsait a szokásos módon $a$, $b$, $c$; $A$, $B$, $C$-vel úgy, hogy $c>b\ge a$ teljesüljön. A $C$ csúcsból induló magasság, szögfelező és súlyvonal legyen $m$, $f$ és $s$, ezek talppontjai pedig $T$, $L$ és $F$ (lásd az ábrát). Nyilvánvaló, hogy $f\ge m$. A szögfelezőtétel szerint $\begin{array}{c}{\displaystyle \frac{b}{a}=\frac{AL}{BL}\mathrm{,}\text{azaz}b\ge a\text{miatt}AL\ge BL\mathrm{.}}\end{array}$ Ugyanakkor a $b\ge a$ egyenlőtlensegből következik, hogy $ABC\sphericalangle \ge BAC\sphericalangle$, vagyis $ABC\sphericalangle \ge \frac{{90}^{\circ }}{2}={45}^{\circ }$, tehát $BCT\sphericalangle =\frac{{90}^{\circ }}{2}={45}^{\circ }$. Ezek alapján $L$-nek $T$ és $F$ között kell elhelyezkednie. Mivel $FLC\sphericalangle =LTC\sphericalangle +TCL\sphericalangle ={90}^{\circ }+TCL\sphericalangle$, ezért az $FLC$ ‐ esetleg elfajuló ‐ háromszögben $FC$ a legnagyobb oldal, azaz $s\ge f$. Viszont Thalész tétele miatt $s=\frac{c}{2}$, tehát $\begin{array}{c}{\displaystyle f+m\le s+s=c\mathrm{.}}\end{array}$ Egyenlőség pontosan akkor áll fenn, ha $s=f=m$, azaz ha a háromszög egyenlő szárú (és természetesen derékszögű).  Hesz Gábor (Budapest, Fazekas M. Gyak. Gimn., II.o.t.) és    Savanya Márta (Bonyhád, Petőfi S. Ev. Gimn., II.o.t.) dolgozatai alapján   II. megoldás. Használjuk az I. megoldás jelöléseit. Az $ABC$ háromszög területét kétféleképpen felírva kapjuk, hogy $\frac{a\cdot b}{2}=\frac{m\cdot c}{2}$, amiből $\begin{array}{c}{\displaystyle m=\frac{a\cdot b}{c}\mathrm{.}}\end{array}$ (1) Az $ABC$ háromszög területét felírhatjuk úgy is, mint az $ALC$ és a $BLC$ háromszögek területeinek összegét: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{c}\hfill {\displaystyle \left(2\right)\frac{a\cdot b}{2}=\frac{a\cdot f\cdot \text{sin}{45}^{\circ }}{2}+\frac{b\cdot f\cdot \text{sin}{45}^{\circ }}{2}\mathrm{,}}\end{array}}}\end{array}$ amiből $f=\frac{\sqrt[]{2}\cdot ab}{a+b}$. Az $a$ és $b$ pozitív számok harmonikus, mértani, számtani és négyzetes közepei közti ismert egyenlőtlenségek szerint $\begin{array}{c}{\displaystyle \frac{2ab}{a+b}\le \sqrt[]{ab}\le \frac{a+b}{2}\le \sqrt[]{\frac{a^2+b^2}{2}}\mathrm{.}}\end{array}$ Ezeket az egyenlőtlenségeket és a Pitagorasz tételéből következő $c=\sqrt[]{a^2+b^2}$ összefüggést (1)-be és (2)-be beírva kapjuk, hogy $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{c}\hfill {\displaystyle \left(3\right)m=\frac{a\cdot b}{c}=\frac{a\cdot b}{\sqrt[]{a^2+b^2}}\le \frac{{\left(\frac{a+b}{2}\right)}^2}{\sqrt[]{2}\cdot \sqrt[]{\frac{a^2+b^2}{2}}}\le \frac{{\left(\frac{a+b}{2}\right)}^2}{\sqrt[]{2}\cdot \frac{a+b}{2}}=\frac{a+b}{2\sqrt[]{2}}\mathrm{,}}\end{array}}}\end{array}$ és $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{c}\hfill {\displaystyle \left(4\right)f=\frac{\sqrt[]{2}a\cdot b}{a+b}\le \frac{\sqrt[]{2}\cdot {\left(\frac{a+b}{2}\right)}^2}{a+b}=\frac{a+b}{2\sqrt[]{2}}\mathrm{.}}\end{array}}}\end{array}$ (3) és (4) megfelelő oldalait összeadva: $\begin{array}{c}{\displaystyle m+f\le \frac{a+b}{\sqrt[]{2}}\le \sqrt[]{2}\sqrt[]{\frac{a^2+b^2}{2}}=c\mathrm{,}}\end{array}$ ami éppen a bizonyítandó állítás. Egyenlőség pontosan akkor áll fenn, ha $a=b$.