Kezdőlap


Feladat:	Gy.3075	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Lengyel Tímea , Nagy Máté
Füzet:	1997/május, 278 - 279. oldal		PDF \| MathML
Témakör(ök):	Egyenlő szárú háromszögek geometriája, Körülírt kör, Hossz, kerület, Gyakorlat
Hivatkozás(ok):	Feladatok: 1996/szeptember: Gy.3075

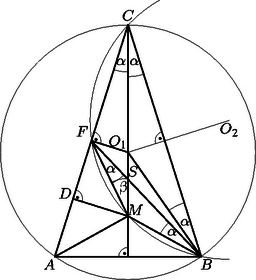
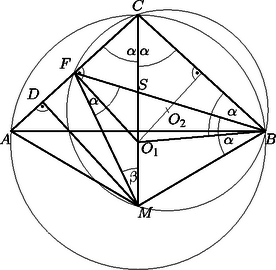
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük az $A C$ szár felezőpontját $F$ -fel, az $A B C$ háromszög köré írható kör középpontját $O_{1}$ -gyel, a $B C F$ háromszög köré írt kör és a $C O_{1}$ egyenes $C$ -től különböző metszéspontját $M$ -mel, az $M$ -ből $A C$ -re bocsátott merőleges talppontját pedig $D$ -vel (az 1. ábra a hegyes-, a 2. pedig a tompaszögű $A B C$ háromszög esetét mutatja).

Mivel a

B

C

F

M

pontok egy körön vannak, azért

M F B ∢ = M C B ∢

és

M B F ∢ = M C F ∢

. Az

A B C

egyenlő szárú háromszögben

M C

felezi az

A C B

szöget, ezért

M C B ∢ = M C A ∢ (= M C F ∢)

, tehát az

M B F

háromszög

B F

oldalán lévő szögek is egyenlők, így

M F = M B

. Az

M

rajta van az

A B C

háromszög szimmetriatengelyén, ezért

M B = M A

, vagyis az

A M F

háromszög is egyenlő szárú, s így

D

felezi az

A F

szakaszt. Mivel

A F = \frac{A C}{2}

, azért

D F = \frac{A C}{4}

. Az

O_{1}

pont rajta van az

A C

szakasz felezőmerőlegesén, ezért

O_{1} F