Feladat: Gy.3068 Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Benedek Csaba ,  Bérczi Gergely ,  Gyenes Zoltán ,  Győri Nikolett ,  Hangya Balázs ,  Juhász András ,  Katona Zsolt ,  Lippner Gábor ,  Szabados Péter ,  Terék Zsolt ,  Zawadowski Ádám 
Füzet: 1997/február, 81 - 82. oldal  PDF  |  MathML 
Témakör(ök): Háromszögek szerkesztése, Diszkusszió, Gyakorlat
Hivatkozás(ok):Feladatok: 1996/május: Gy.3068

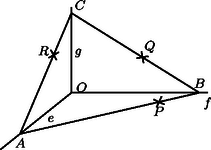
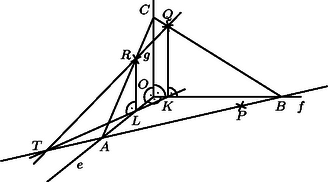
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Tekintsük a feladatot megoldottnak. Jelöljük az e, f, g közös kezdőpontját O-val, a szerkesztendő háromszög csúcsait A, B, C-vel, az adott pontokat pedig P, Q, R-rel (1. ábra). Tegyük fel, hogy az e, f, g félegyenesek nincsenenk egy síkban. Jelöljük az általunk páronként meghatározott síkokat Sef, Sfg és Seg-vel, ABC síkját pedig S-sel. Mivel R∈Seg és Q∈Sfg, azért az R-en, illetve Q-n átmenő, g-vel párhuzamos egyenesek az L∈Seg, illetve a K∈Sfg pontban metszik e-t, illetve f-et (2. ábra). Mivel RL‖g‖QK, azért az R, L, K, Q pontok egy S' síkban vannak. Ha P, Q és R közül egyik sem esik egybe ABC csúcsaival, akkor S' különbözik S-től is és Sef-től is, tehát AB, RQ és LK a páronkénti metszésvonalai az S, S' és Sef síkoknak. Ha e három egyenes közül valamelyik kettő egy T pontban metszi egymást, akkor T az S, S' és Sef síkok mindegyikén rajta van, azaz a három sík közös pontja, tehát a harmadik síkpár metszésvonala is átmegy rajta. Ezzel beláttuk, hogy AB, LK és RQ vagy egy ponton mennek át, vagy párhuzamosak. Ez az állítás akkor is igaz, ha az e, f, g félegyenesek egy síkban vannak. Ennek bizonyítását az olvasóra hagyjuk. (Egy lehetséges bizonyítási mód: az e, f, g félegyenesekhez konstruáljunk olyan e', f', g' félegyeneseket, amelyek nincsenek egy síkban, és egy megfelelő irányból egy síkra vetítve őket, a vetületük éppen e, f és g.)
A szerkesztést tehát a következő módon végezhetjük: R-en és Q-n át párhuzamosokat szerkesztünk g-vel, ezek L-ben, illetve K-ban metszik e-t és f-et. RQ és LK T metszéspontját összekötjük P-vel (ha RQ‖LK, akkor P-n át ezekkel párhuzamost húzunk), ez A-ban és B-ben metszi e-t, illetve f-et. Végül BQ és AR metszéspontja adja a ‐ g-n lévő ‐ C csúcsot. Az így szerkesztett ABC háromszög C csúcsa mindig g-n lesz, mert RL‖g‖QK, és az RQ, LK és AB egyenesek pedig vagy egy ponton mennek át, vagy párhuzamosak. A megoldások száma az adott pontok és félegyenesek kölcsönös helyzetétől függően legfeljebb 6 (szerkesztésünk csak azt biztosítja, hogy a háromszög csúcsai a félegyeneseket tartalmazó egyeneseken vannak, illetve hogy a háromszög oldalegyenesei átmennek az adott pontokon).
 Szabados Péter (Dombóvár, Illyés Gy. Gimn., II. o.t.) dolgozata alapján