Kezdőlap


Feladat:	Gy.3066	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bérczi Gergely , Lippner Gábor
Füzet:	1997/január, 20 - 21. oldal		PDF \| MathML
Témakör(ök):	Háromszögek nevezetes tételei, Másodfokú (és arra visszavezethető) egyenlőtlenségek, Beírt kör, Ellenpélda, mint megoldási módszer a matematikában, Gyakorlat
Hivatkozás(ok):	Feladatok: 1996/május: Gy.3066

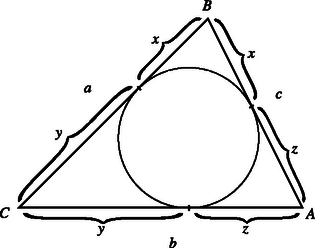
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen $a = x + y$ , $b = y + z$ , $c = z + x$ , ahol $x$ , $y$ és $z$ a háromszög csúcsaiból a beírt körhöz húzható érintőszakaszok hosszai (l. az ábrát), tehát $x$ , $y$ , $z > 0$ . Így a bizonyítandó állítás:

\begin{matrix} {[2 (x + y + z)]}^{2} < 4 ((x + y) (y + z) + (y + z) (z + x) + (z + x) (x + y)) . \end{matrix}

(1)

Ez a műveleteket elvégezve, majd egyszerűsítve 4-gyel és rendezve a nyilvánvalóan teljesülő

\begin{matrix} 0 < x y + y z + z x \end{matrix}

egyenlőtlenséggé válik. Mivel ekvivalens átalakításokat végeztünk, azért az eredeti egyenlőtlenség is teljesül.
Megmutatjuk, hogy ha

ε > 0

tetszőleges szám, akkor van olyan háromszög, amelynek oldalai nem elégítik ki az

\begin{matrix} {(a + b + c)}^{2} < (4 - ε) (a b + b c + c a) \end{matrix}

egyenlőtlenséget. Az (1) egyenlőtlenségben 4 helyett

(4 - ε)

-t írva és rendezve kapjuk, hogy

\begin{matrix} x^{2} + y^{2} + z^{2} < \frac{4 - 3 ε}{ε} (x y + y z + z x) . \end{matrix}

(2)

Legyen

x = y = \sqrt[]{\frac{ε}{8}}

és

z = \sqrt[]{\frac{8}{ε}}

. Ezeket az értékeket (2)-be helyettesítve kapjuk, hogy

\begin{matrix} \frac{ε}{8} + \frac{ε}{8} + \frac{8}{ε} < \frac{4 - 3 ε}{ε} (\frac{ε}{8} + 2) = \frac{1}{2} + \frac{8}{ε} - \frac{3 ε}{8} - 6. \end{matrix}

Ez pedig nyilvánvalóan nem igaz, mert

ε > 0

.
Tehát, ha pl.

ε = 0,5

, akkor az

a = 0,5

b = c = 4,25

egység oldalú háromszög oldalaira nem teljesül az

{(a + b + c)}^{2} < 3,9 (a b + b c + c a)

egyenlőtlenség.

Lippner Gábor (Fazekas M. Főv. Gyak. Gimn., II. o.t.) dolgozata alapján