Kezdőlap


Feladat:	Gy.3050	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bérczi Gergely , Davidovics Gábor , Lippner Gábor , Szabó István , Varga Csilla
Füzet:	1996/december, 523 - 524. oldal		PDF \| MathML
Témakör(ök):	Háromszögek nevezetes tételei, Egyenlő szárú háromszögek geometriája, Gyakorlat
Hivatkozás(ok):	Feladatok: 1996/március: Gy.3050

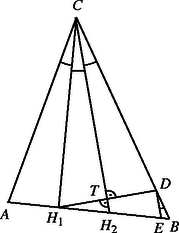
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöljük az $A B C$ háromszög $C$ -nél lévő szögének harmadolói és a háromszög $A B$ oldalának metszéspontjait $H_{1}$ -gyel és $H_{2}$ -vel. A $H_{1} C H_{2}$ háromszögben legfeljebb egy tompaszög van. A $C$ csúcsnál lévő szög biztosan hegyesszög, mert $H_{1} C H_{2} ∢ = \frac{1}{3} A C B ∢ < \frac{1}{3} \cdot 180^{\circ} = 60^{\circ}$ ; feltehetjük, hogy a $H_{2}$ -nél lévő szög is hegyesszög. Ekkor a $H_{1}$ -ből a $H_{2} C$ egyenesre állított merőleges a $H_{2} C$ szakaszt annak egy belső $T$ pontjában metszi (l. az ábrát). Ebből következik, hogy a merőleges a $B C$ szakaszt is egy belső pontban, $D$ -ben metszi.
A $H_{1} D C$ háromszög egyenlő szárú (mert $C$ -hez tartozó szögfelezője egyúttal magasságvonal is), ezért egyrészt $H_{1} D C ∢ < 90^{\circ}$ , így a $H_{1} D$ -re $D$ -ben állított merőleges a $H_{1} B$ szakaszt egy belső $E$ pontban metszi; másrészt $H_{1} T = T D$ , amiből $T H_{2} ‖ D E$ miatt következik, hogy $H_{1} H_{2} = H_{2} E$ . Ez viszont azt mutatja, hogy $H_{1} H_{2} < H_{2} B$ .
Tehát a három szakasz közül nem lehet a középső a leghosszabb.

Varga Csilla (Budapest, Eötvös J. Gimn., I. o.t.) dolgozata alapján

Megjegyzés. Hasonló módon belátható, hogy ha egy háromszög egyik szögét

n

egyenlő részre osztó egyenesek által a szemközti oldalon alkotott

n

szakaszt nézzük, akkor ezek közül valamelyik szélső lesz a legnagyobb.