Kezdőlap


Feladat:	Gy.3045	Korcsoport: 16-17	Nehézségi fok: nehéz
Megoldó(k):	Barát Anna , Bérczi Gergely , Győri Nikolett , Juhász András , Lippner Gábor , Méder Áron , Nagy Endre , Páles Csaba
Füzet:	1996/december, 519 - 520. oldal		PDF \| MathML
Témakör(ök):	Tetraéderek, Beírt gömb, Terület, felszín, Térfogat, Gyakorlat
Hivatkozás(ok):	Feladatok: 1996/február: Gy.3045

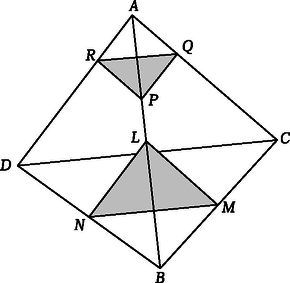
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Megmutatjuk, hogy ha egy tetraéder lapjai nem egyenlő területűek, akkor a két legkisebb területű lappal szemközti csúcsoknál lévő kis tetraédereknek van közös belső pontjuk.
Tegyük fel, hogy az $A B C D$ tetraéder $B C D$ és $A C D$ lapjai a legkisebb területűek. Az $A$ és a $B$ csúcsokhoz tartozó kis tetraéderek további csúcsait jelölje az ábra szerint $P$ , $Q$ , $R$ , illetve $L$ , $M$ és $N$ . Megmutatjuk, hogy $A P + L B > A B$ , amiből állításunk nyilván következik.
A $P Q R$ és a $B C D$ síkok párhuzamosak, ezért az $A B C D$ és az $A P Q R$ tetraéderek hasonlók. Ha e két tetraéder $A$ -hoz tartozó magasságát $M_{A}$ , illetve $m_{A}$ jelöli, akkor a hasonlóság miatt

\begin{matrix} \frac{A P}{A B} = \frac{m_{A}}{M_{A}} . \end{matrix}

(1)

Jelöljük a nagy tetraéder térfogatát

V

-vel, beírt gömbjének sugarát

ϱ

-val, az egyes lapok területét pedig

t_{A}

t_{B}

t_{C}

és

t_{D}

-vel. Ismert, hogy

\begin{matrix} 3 V = M_{A} \cdot t_{A} = ϱ (t_{A} + t_{B} + t_{C} + t_{D}) . \end{matrix}

Mivel

P Q R

érinti a beírt gömböt, ezért

M_{A} = m_{A} + 2 ϱ

. Ezeket az összefüggéseket felhasználva alakítsuk át (1)-et:

\begin{matrix} \begin{matrix} \frac{A P}{A B} & = \frac{M_{A} - 2 ϱ}{M_{A}} = \frac{3 V / t_{A} - 2 ϱ}{3 V / t_{A}} = \frac{3 V - 2 ϱ \cdot t_{A}}{3 V} = \\ = \frac{ϱ (t_{A} + t_{B} + t_{C} + t_{D}) - 2 ϱ \cdot t_{A}}{ϱ (t_{A} + t_{B} + t_{C} + t_{D})} = \frac{t_{B} + t_{C} + t_{D} - t_{A}}{t_{A} + t_{B} + t_{C} + t_{D}} . \end{matrix} \end{matrix}

B A C D

és a

B L M N

hasonló tetraéderekből kiindulva ugyanezzel az eljárással azt kapjuk, hogy

\begin{matrix} \frac{B L}{A B} = \frac{t_{A} + t_{C} + t_{D} - t_{B}}{t_{A} + t_{B} + t_{C} + t_{D}} . Vagyis \frac{A P + L B}{A B} = \frac{2 t_{C} + 2 t_{D}}{t_{A} + t_{B} + t_{C} + t_{D}} > 1, \end{matrix}

mert feltételeink szerint

t_{C} + t_{D} > t_{A} + t_{B}

. Így a két tetraédernek van közös belső pontja.

Lippner Gábor (Fazekas M. Főv. Gyak. Gimn., II. o.t.) dolgozata alapján