|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Először megmutatjuk, hogy bármely kijelölt részhalmaznak pontosan eleme van. Mivel valódi részhalmaz, azért létezik egy benne nem lévő elem. Minden elemnek megfeleltetve az (a) szerint egyértelműen létező, -t és -t tartalmazó kijelölt részhalmazt, kölcsönösen egyértelmű megfeleltetést kapunk elemei és a -t tartalmazó, -t metsző kijelölt részhalmazok közt. Tehát minden kijelölt részhalmaz elemet tartalmaz.
A (b) feltételből következik, hogy minden elemet pontosan kijelölt részhalmaz tartalmaz. Rögzítsük most -nak egy elemét. Az -től különböző elemek mindegyike ‐ (a) miatt ‐ pontosan egy -t tartalmazó részhalmazhoz tartozik hozzá. Az -t részhalmaz tartalmazza, és ezek mindegyikében darab -től különböző elem van; ezért -nak összesen eleme van.
A kijelölt részhalmazok száma legyen . Számoljuk össze azon párokat, ahol a -nak egy eleme, egy kijelölt részhalmaz, és . Mivel elemünk van, és mindegyik részhalmazban van benne, azért az ilyen párok száma . A számolást viszont úgy is elvégezhetjük, hogy a darab kijelölt részhalmaz mindegyike elemet tartalmaz, ezért a párok száma . A kétféle számolás eredményének meg kell egyeznie, ezért , ahonnan kapjuk, hogy | |
| Frenkel Péter (Fazekas M. Főv. Gyak. Gimn., III. o.t.) dolgozata alapján |
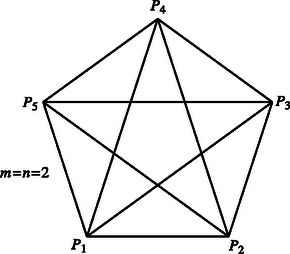
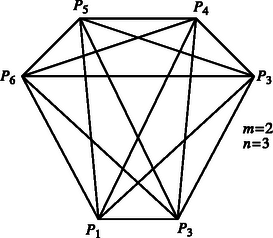
Megjegyzés. A feladathoz nem tartozott hozzá annak vizsgálata, hogy léteznek-e a feltételeknek eleget tevő halmazok. A megoldásból látszik ‐ hiszen -nak egész számnak kell lennie ‐, hogy nem minden párhoz van . A létezés szükséges feltétele, hogy ; általában azonban a létezés kérdése megoldatlan probléma. Az ábrákon két egyszerű példát mutatunk. elemeit pontokkal (, , ) jelöljük, a kitüntetett részhalmazok kételeműek, ezeket úgy adjuk meg, hogy a részhalmazt alkotó két pontot egy egyenessel összekötjük. Az esetén is létezik (13 elemet tartalmaz, és 26 részhalmazt kell kijelölnünk), ennek megadása azonban már nem ilyen egyszerű.
|
 PDF |
PDF |  MathML
MathML