Feladat: Gy.3043 Korcsoport: 16-17 Nehézségi fok: átlagos
Megoldó(k):  Bérczi Gergely ,  Lippner Gábor 
Füzet: 1996/november, 480 - 481. oldal  PDF  |  MathML 
Témakör(ök): Érintőnégyszögek, Trapézok, Alakzatba írt kör, Pitagorasz-tétel alkalmazásai, Háromszögek hasonlósága, Gyakorlat
Hivatkozás(ok):Feladatok: 1996/február: Gy.3043

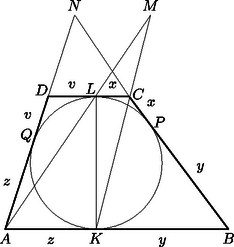
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Jelöjük AD és BC metszéspontját N-nel, AL és KC metszéspontját M-mel ‐ mivel AB≠CD, ezek a metszéspontok léteznek ‐, a kör BC és AD oldalon lévő érintési pontjai pedig legyenek P és Q. A trapéz csúcsaiból a beírt körhöz húzható érintőszakaszok hosszát jelöljük az 1. ábrán látható módon x, y, z és v-vel.
Mivel AB‖CD, azért KL a beírt körnek átmérője, a KBCL négyszög pedig derékszögű trapéz. Messe a C-n átmenő, KL-lel párhuzamos egyenes KB-t T-ben. Ekkor CTB derékszögű háromszög, CB=x+y, TB=|y-x| (2. ábra). Pitagorasz tétele szerint KL=CT=(x+y)2-(x-y)2=2xy. Ugyanezt a gondolatmenetet a KLDA trapézra alkalmazva kapjuk, hogy KL=2vz. Tehát xy=vz.
Jelöljük az M és N pontok CD egyenestől való távolságát m-mel, illetve n-nel. Az AKM és az LCM háromszögek nyilvánvalóan hasonlóak, ezért M-hez tartozó magasságaik aránya megegyezik M-mel szemközti oldalaik arányával:
mm+KL=LCAK=xz.

Az ABN és a DCN háromszögek hasonlóságából pedig azt kapjuk, hogy
nn+KL=CDAB=x+vy+z.
Viszont xy=zv miatt xz=x+vy+z, így
mm+KL=nn+KL.
Ebből viszont következik, hogy m=n.
Ezzel beláttuk, hogy MN párhuzamos a trapéz alapjaival.
 Lippner Gábor (Fazekas M. Főv. Gyak. Gimn,. II. o.t.)