Kezdőlap


Feladat:	Gy.3036	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bárány Zsófi , Bérczi Gergely , Gyenes Zoltán , Hartmann Miklós , Juhász András , Lippner Gábor , Nagy Endre , Paál Krisztina , Pap Júlia , Szalai-Dobos András , Vaik István , Végh László , Zábrádi Gergely
Füzet:	1996/október, 414 - 416. oldal		PDF \| MathML
Témakör(ök):	Mértani sorozat, Érintőnégyszögek, Háromszögek hasonlósága, Pitagorasz-tétel alkalmazásai, Gyakorlat
Hivatkozás(ok):	Feladatok: 1996/január: Gy.3036

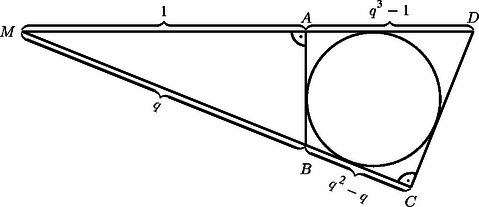
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az $M A$ távolságot választhatjuk $1$ -nek. Jelöljük $q$ -val a feladatban szereplő mértani sorozat hányadosát. Ekkor $M B = q$ , $M C = q^{2}$ és $M D = q^{3}$ . Ha $M A \geq M B$ , akkor nincs mit bizonyítanunk. Ha $M A < M B < M C < M D$ , akkor a pontok az ábrán látható módon helyezkednek el.
Mivel $M A B ∢ = 180^{\circ} - B A D ∢ = 90^{\circ}$ , ezért az $M A B$ háromszög $A B$ oldalát Pitagorasz tétele segítségével határozhatjuk meg:

\begin{matrix} A B = \sqrt[]{M B^{2} - M A^{2}} = \sqrt[]{q^{2} - 1} . \end{matrix}

M A B

és az

M C D

háromszögek hasonlóak, mert

\frac{M A}{M B} = \frac{M C}{M D}

és

A M B ∢ = D M C ∢

. Így

M C D ∢ = M A B ∢ = 90^{\circ}

, tehát a

C D

oldalt is meghatározhatjuk Pitagorasz tétele segítségével:

\begin{matrix} C D = \sqrt[]{M D^{2} - M C^{2}} = \sqrt[]{q^{6} - q^{4}} = q^{2} \sqrt[]{q^{2} - 1} . \end{matrix}

A B C D

négyszög érintőnégyszög, ezért szemközti oldalainak összege egyenlő:

\begin{matrix} \begin{matrix} A B + C D = A D + B C = (M D - M A) + (M C - M B), azaz \\ \sqrt[]{q^{2} - 1} + q^{2} \sqrt[]{q^{2} - 1} = q^{3} - 1 + q^{2} - q . \end{matrix} \end{matrix}

Ebből kapjuk, hogy

\begin{matrix} (q^{2} + 1) \sqrt[]{q^{2} - 1} = (q^{2} - 1) (q + 1) . \end{matrix}

Négyzetre emelve, majd

0 \neq (q^{2} - 1)

-gyel elosztva és rendezve:

\begin{matrix} q^{3} = q^{2} + q + 1 \end{matrix}

(1)

Tegyük fel, hogy

q > 2

. Ekkor

\begin{matrix} q^{3} > 2 q^{2}, \end{matrix}

\begin{matrix} q^{2} > 2 q, \end{matrix}

\begin{matrix} q > 2. \end{matrix}

Ezeket összeadva:

q^{3} + q^{2} + q > 2 q^{2} + 2 q + 2

, azaz

q^{3} > q^{2} + q + 2

. Tehát az (1) egyenletnek nincs

2

-nél nagyobb gyöke, vagyis a feladatban szereplő mértani sorozat hányadosa

2

-nél kisebb.

Nagy Endre (Szekszárd, Garay J. Gimn., II. o.t.) dolgozata alapján

Megjegyzés. Megoldásunkban nem szóltunk arról, hogy a feladatban szereplő

A B C D

négyszög létezik-e. Azt mutattuk meg, hogy ha létezik ilyen négyszög, akkor

q < 2

. Meg lehet mutatni, hogy valóban van ilyen négyszög (

q

értéke

\approx 1,84