Kezdőlap


Feladat:	Gy.3034	Korcsoport: 16-17	Nehézségi fok: átlagos
Megoldó(k):	Bérczi Gergely , Hangya Balázs , Katona Zsolt , Kolozs Anita , Pogány Ádám , Szalai-Dobos András , Vaik István , Végh László
Füzet:	1996/október, 412 - 413. oldal		PDF \| MathML
Témakör(ök):	Téglalapok, Hossz, kerület, Gyakorlat
Hivatkozás(ok):	Feladatok: 1996/január: Gy.3034

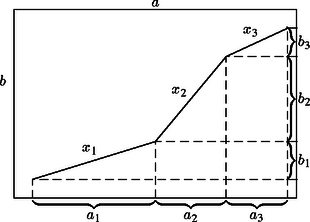
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyenek a töröttvonal szakaszai $x_{1}$ , $x_{2}$ , $...$ , $x_{n}$ ; a téglalap két szomszédos oldala $a$ és $b$ ; az $x_{i}$ szakasz merőleges vetülete az $a$ oldalon $a_{i}$ , a $b$ oldalon pedig $b_{i}$ . Mivel a $b$ oldallal párhuzamos bármely egyenes legfeljebb egyszer metszi a töröttvonalat, ezért az $a_{i}$ szakaszok között nincs átfedés, azaz

\begin{matrix} a_{1} + a_{2} + ... + a_{n} < a . \end{matrix}

Ugyanígy láthatjuk be, hogy

\begin{matrix} b_{1} + b_{2} + ... b_{n} < b . \end{matrix}

A merőleges vetítés miatt

x_{i}

átfogója egy olyan derékszögű háromszögnek, amelynek egyik befogója

a_{i}

, a másik pedig

b_{i}

(a feltételek szerint

x_{i}

nem lehet párhuzamos a téglalap egyik oldalával sem, ezért ezek a háromszögek nem elfajulók). Ezért a háromszög-egyenlőtlenség alapján

x_{i} < a_{i} + b_{i}

minden

i

-re. Ezeket összeadva kapjuk, hogy

\begin{matrix} \begin{matrix} x_{1} + x_{2} + ... + x_{n} & < (a_{1} + b_{1}) + (a_{2} + b_{2}) + ... + (a_{n} + b_{n}) = \\ = (a_{1} + a_{2} + ... + a_{n}) + (b_{1} + b_{2} + ... + b_{n}) < a + b, \end{matrix} \end{matrix}

ami éppen a bizonyítandó állítás.

Katona Zsolt (Fazekas M. Főv. Gyak. Gimn., II. o.t.)

Megjegyzés. A 0 pontos dolgozatokban szereplő ,,töröttvonalak'' nem teljesítették a gyakorlat első mondatában megfogalmazott feltételt!