Feladat:	F.3147	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Barát Anna ,  Bérczi Gergely ,  Czirok Levente ,  Gyurkó L. Gergely ,  Györkei Györgyi ,  Horváth Gábor ,  Jeszenszky Gyula ,  Juhász András ,  Kürthy Gábor ,  Léka Zoltán ,  Lippner Gábor ,  Megyeri Csaba ,  Nagy István ,  Németh András ,  Nyakas Péter ,  Oláh Szabolcs ,  Páles Csaba ,  Pintér Dömötör ,  Pogány Ádám ,  Rudolf Gábor ,  Salamon Gábor ,  Szalai-Dobos András ,  Szilágyi Judit ,  Szűcs Gábor ,  Terék Zsolt ,  Terpai Tamás ,  Várkonyi Péter ,  Vörös Imre
Füzet:	1997/április, 222 - 224. oldal		PDF  |  MathML
Témakör(ök):	Tetraéderek, Szögfüggvények a térben, Terület, felszín, Háromszögek nevezetes tételei, Számtani-mértani egyenlőtlenségek, Feladat
Hivatkozás(ok):	Feladatok: 1996/november: F.3147

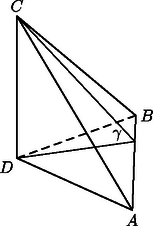
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Jelöljük az $ABC$ lap területét $t$-vel. Vetítsük rá az $ABC$ háromszöget a másik három lapra. Ha pl. az $ABC$ lap az $ABD$-vel $\gamma$ szöget zár be (1. ábra), akkor $t\cdot \text{cos}\gamma =\frac{1}{2}DA\cdot DB$. Hasonlóan kapjuk, hogy $t\cdot \text{cos}\alpha =\frac{1}{2}\cdot DB\cdot DC$ és $t\cdot \text{cos}\beta =$ =12⋅DC⋅DA. A három összefüggés szorzatából: $\begin{array}{c}{\displaystyle t^3\cdot \text{cos}\alpha \cdot \text{cos}\beta \cdot \text{cos}\gamma =\frac{1}{8}{\left(DA\cdot DB\cdot DC\right)}^2\mathrm{.}}\end{array}$ (1) Vetítsük most a $D$ csúcsot tartalmazó lapokat az $ABC$-re. A vetületek területének összege nyilván $t$, ezért $\begin{array}{c}{\displaystyle t=\frac{1}{2}DA\cdot DB\text{cos}\gamma +\frac{1}{2}DB\cdot DC\text{cos}\alpha +\frac{1}{2}DC\cdot DA\text{cos}\beta \mathrm{.}}\end{array}$ A számtani és mértani közép közötti összefüggés szerint, felhasználva, hogy $\alpha$, $\beta$, $\gamma$ mindegyike hegyesszög, $\begin{array}{c}{\displaystyle \frac{t}{3}\ge \sqrt[3]{\frac{1}{8}{\left(DA\cdot DB\cdot DC\right)}^2\cdot \text{cos}\alpha \cdot \text{cos}\beta \cdot \text{cos}\gamma }\mathrm{,}}\end{array}$ majd (1) alapján $\begin{array}{c}{\displaystyle \frac{t}{3}\ge \sqrt[3]{t^3\text{cos}{}^2\alpha \cdot \text{cos}{}^2\beta \cdot \text{cos}{}^2\gamma }\mathrm{,}}\end{array}$ amiből $\text{cos}\alpha \cdot \text{cos}\beta \cdot \text{cos}\gamma \le \frac{\sqrt[]{3}}{9}$. Egyenlőség pontosan akkor van, ha $\text{cos}\alpha =\text{cos}\beta =\text{cos}\gamma$, tehát ha az $ABC$ háromszög szabályos.  Páles Csaba (Debrecen , KLTE Gyak. Gimn., III. 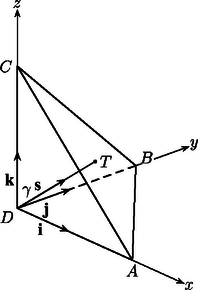o.t.)   II. megoldás. Legyen a tetraéder $D$ csúcsa egy derékszögű koordináta-rendszer kezdőpontja, az $A$, $B$, $C$ csúcsok pedig illeszkedjenek az $x$, $y$, $z$ tengelyekre (2. ábra). Legyen továbbá a tetraéder $D$ csúcsából induló magasság talppontja $T$, a $DT$-re illeszkedő egységvektor $\text{s}$. Használjuk az ábra további jelöléseit is. Ha az $ABD$ és $ABC$ lap hajlásszöge $\gamma$, akkor a $CDT$ szög is $\gamma$, hiszen $CD$ az $ABD$ sík, $DT$ pedig az $ABC$ sík normálisa. Hasonlóan kapjuk, hogy $ADT\sphericalangle =\alpha$ és $BDT\sphericalangle =\beta$. Könnyen látható, hogy $\text{cos}\alpha =\text{i}\cdot \text{s}$, $\text{cos}\beta =\text{j}\cdot \text{s}$ és $\text{cos}\gamma =\text{k}\cdot \text{s}$, és így $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle \text{cos}\alpha +\text{cos}\beta +\text{cos}\gamma }& {\displaystyle =\left(\text{i}+\text{j}+\text{k}\right)\cdot \text{s}=}\hfill \\ \hfill {\displaystyle =1\cdot \sqrt[]{3}\cdot \text{cos}\phi }& {\displaystyle \le \sqrt[]{3}\mathrm{,}}\hfill & \hfill {\displaystyle \left(2\right)}\end{array}}}\end{array}$ ahol $\phi$ az $\text{s}$ és az $\text{i}+\text{j}+\text{k}$ vektorok szöge. A számtani és mértani közép közötti egyenlőtlenség és (2) szerint: $\begin{array}{c}{\displaystyle \text{cos}\alpha \cdot \text{cos}\beta \cdot \text{cos}\gamma \le {\left(\frac{\text{cos}\alpha +\text{cos}\beta +\text{cos}\gamma }{3}\right)}^3\le {\left(\frac{\sqrt[]{3}}{3}\right)}^3=\frac{\sqrt[]{3}}{9}\mathrm{,}}\end{array}$ (3) ahol felhasználtuk, hogy $\alpha$, $\beta$, $\gamma$ mindegyike hegyesszög. Egyenlőség (2)-ben és (3)-ban is akkor és csak akkor áll fenn, ha $\alpha =\beta =\gamma$, azaz $DA=DB=DC$, amikoris az $ABC$ háromszög szabályos.  Bérczi Gergely (Szeged, Ságvári E. Gyak. Gimn., III. o.t.)   III. megoldás. A 2. ábra s egységvektorának koordinátái $\text{cos}\alpha$, $\text{cos}\beta$, $\text{cos}\gamma$, ezért $\text{cos}{}^2\alpha +\text{cos}{}^2\beta +\text{cos}{}^2\gamma =1$. A mértani és négyzetes közepek közötti egyenlőtlenség szerint: $\begin{array}{c}{\displaystyle \sqrt[3]{\text{cos}\alpha \cdot \text{cos}\beta \cdot \text{cos}\gamma }\le \sqrt[]{\frac{\text{cos}{}^2\alpha +\text{cos}{}^2\beta +\text{cos}{}^2\gamma }{3}}=\sqrt[]{\frac{1}{3}}\mathrm{,}}\end{array}$ amiből már következik a feladat állítása.