Feladat: F.3145 Korcsoport: 18- Nehézségi fok: nehéz
Megoldó(k):  Bérczi Gergely ,  Dedinszky Zsófia ,  Devecsery András ,  Fazekas Borbála ,  Gyenes Zoltán ,  Gyurkó L. Gergely ,  Héjjas Péter ,  Juhász András ,  Karádi Richárd ,  Lázár Zsófia ,  Lippner Gábor ,  Méder Áron ,  Megyeri Csaba ,  Páles Csaba ,  Patakfalvi Zsolt ,  Pintér Dömötör ,  Prohászka Benedek ,  Szabó Előd ,  Szita István ,  Szűcs Gábor ,  Terék Zsolt ,  Terpai Tamás 
Füzet: 1997/december, 538 - 540. oldal  PDF  |  MathML 
Témakör(ök): Háromszögek nevezetes tételei, Körülírt kör, Kör geometriája, Feuerbach-kör, Feladat
Hivatkozás(ok):Feladatok: 1996/november: F.3145

A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

A feladat megoldásához szükségünk lesz a következő segédtételre: Legyen a k és k' körök metszéspontja E és F. Az E ponton átmenő tetszőleges e egyenes messe a k kört P-ben, k'-t pedig Q-ban. Bizonyítsuk be, hogy a PQ szakasz O felezőpontja bármely e esetén illeszkedik egy az E és F pontokon átmenő fix K 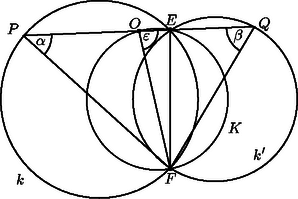körre.

 
 

Az FPQ háromszögben OPF∢=α állandó (kerületi szög), hasonlóképpen PQF∢=β is állandó, vagyis független a P és Q pontok helyzetétől.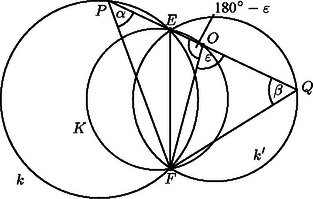
 
 

Ebből következik, hogy a QOF∢=ε is állandó. Az O felezőpont tehát rajta van az EF szakasz fölé írt ε szögű látóköríven. Mégpedig, ha O a k körbe esik és k elválasztja P-t és Q-t, O a látókörívnek a k körbe eső EF ívén van (1. ábra). Ha viszont a PQ szakasz felezőpontja a k' körbe esik és k elválasztja P-t és Q-t, akkor O az előbb mondott látókörív kiegészítő ívén lesz rajta (2. ábra). Ennek igazolását könnyen leolvashatjuk a 2. ábráról, hiszen most az EF szakasz O-ból 180∘-ε szög alatt látszik.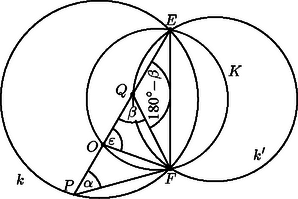
 
 

Meg kell vizsgálnunk még azokat az eseteket, amikor k nem választja el a P és Q pontokat. Essen most P és Q a k körbe. A PFQ háromszög két szöge most is α és β (állandó), ezért az EF szakasz ε szögű látóköre átmegy az O ponton. Ha P és Q a k' körbe esik, teljesen hasonló a bizonyítás az előzőhöz, O mértani helye most is a kiegészítő körív. A keresett fix kör tehát valóban létezik.
Ezután térjünk rá a feladat állításának bizonyítására. A Feuerbach-kör egy háromszögnek az a köre, amely átmegy a háromszög oldalainak felezőpontján, a magasságok talppontjain és a magasságvonalaknak a csúcs és magasságpont közé eső szakaszainak felezőpontján. (Ez összesen 9 pont, ezért is szokták a Feuerbach-kört 9 pontos körnek is nevezni.) E 9 pont közül bármely 3 már meghatározza a kört.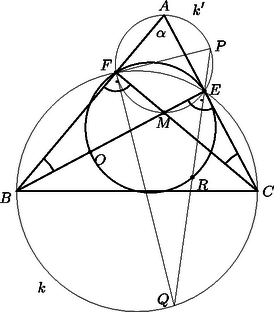
 
 

Az ABC háromszög magasságai BE és CF (4. ábra), metszéspontjuk M. Az AEMF húrnégyszög körülírt köre k', az ABC háromszög BC oldala, mint átmérő fölé írt kör k. Az E és F pontok és a BM szakasz O felezőpontja meghatározza az ABC háromszög Feuerbach-körét. A BM egyenes is és a PQ egyenes is megfelel a segédtételben használt e egyenesek egyikének, így a segédtétel szerint PQ felezőpontja, R ugyanazt a kört határozza meg az E és F pontokkal, mint O, s ez a kör az ABC háromszög Feuerbach-köre. Ha a háromszög tompaszögű, akkor A és M szerepet cserél, s a bizonyítás ugyanígy elvégezhető. Ezzel a feladat állítását igazoltuk.