Feladat:	F.3140	Korcsoport: 16-17	Nehézségi fok: könnyű
Megoldó(k):	Bérczi Gergely ,  Czirok Levente ,  Jakabfy Tamás ,  Lobozár Ferenc ,  Pogány Ádám ,  Terék Zsolt ,  Terpai Tamás ,  Zsombori Gabriella
Füzet:	1997/április, 216 - 218. oldal		PDF  |  MathML
Témakör(ök):	Kör geometriája, Koszinusztétel alkalmazása, Feladat
Hivatkozás(ok):	Feladatok: 1996/október: F.3140

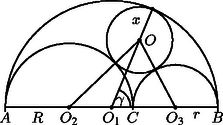
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Legyen az érintő kör sugara $x$. Használjuk az 1. ábra további jelöléseit. Az $O_2{O}_{1}O$ és $O_1{O}_{3}O$ háromszögekre a koszinusztételt fölírva: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle {\left(R+x\right)}^2}& {\displaystyle ={\left(R+r-x\right)}^2+r^2+2\left(R+r-x\right)\cdot r\cdot \text{cos}\gamma \mathrm{,}}\hfill \\ \hfill {\displaystyle {\left(r+x\right)}^2}& {\displaystyle ={\left(R+r-x\right)}^2+R^2-2\left(R+r-x\right)\cdot R\cdot \text{cos}\gamma \mathrm{.}}\hfill \end{array}}}\end{array}$ Szorozzuk meg az első egyenletet $R$-rel, a másodikat $r$-rel, majd adjuk össze őket: $\begin{array}{c}{\displaystyle {\left(R+x\right)}^{2}R+{\left(r+x\right)}^{2}r={\left(R+r-x\right)}^2\left(R+r\right)+r^{2}R+r{R}^2\mathrm{,}}\end{array}$ (1) amiből némi számolással: $\begin{array}{c}{\displaystyle x=\frac{Rr\left(R+r\right)}{R^2+Rr+r^2}\mathrm{.}}\end{array}$  Lobozár Ferenc (Szeged, Csonka J. Műsz. Szki., III. o.t.)   II. megoldás. R. Descartes-tól származik a következő tétel: ha négy kör bármelyike érinti a másik hármat, akkor görbületeik négyzetösszegének kétszerese egyenlő a görbületeinek összegének négyzetével. Az $r$ sugarú kör görbülete $\frac{1}{r}$, az egyenes görbülete zérus. A tétel akkor is érvényes, ha valamelyik kör helyett egyenes szerepel. Alkalmazása szempontjából az egymást kívülről érintő körök görbülete azonos előjelű, a belülről érintőké egymással ellentétes. Bizonyítása megtalálható H. S. M. Coxeter: A geometriák alapjai c. könyv 31‐32. oldalán. A tétel alapján: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{c}\hfill {\displaystyle 2\left(\frac{1}{r^2}+\frac{1}{R^2}+\frac{1}{{\left(r+R\right)}^2}+\frac{1}{x^2}\right)={\left(\frac{1}{r}+\frac{1}{R}-\frac{1}{r+R}+\frac{1}{x}\right)}^2\mathrm{.}}\end{array}}}\end{array}$ Ezt az $\frac{1}{x}$-re másodfokú egyenletet megoldva $x$ meghatározható: $\begin{array}{c}{\displaystyle x=\frac{Rr\left(R+r\right)}{R^2+Rr+r^2}\mathrm{.}}\end{array}$  Terék Zsolt (Fazekas M. Főv. Gyak. Gimn., III. o.t.)   Megjegyzések. 1. Descartes idézett tétele az idők során feledésbe merült, majd többen is újra felfedezték, pl. 1936-ban Sir Frederick Soddy ‐ Nobel-díjas fizikus ‐, aki azt is megmutatta, hogy analóg tétel érvényes a térben 5 gömbre. A tételekről Precíz csók címmel verset írt, amelynek egyik versszaka így fogalmazza meg a 2. megoldásban felhasznált tételt:     Egymásnak négy kör csókot ad, a kisebbik hajlik jobban; a görbület a központból mért táv, de reciprokban. Nem bírt vele Euklid' esze, az ujjszabály sem szól bele; mert nem görbül az egyenes s a konkáv hajlás mínusz lesz, a négy görbület négyzetösszege épp a görbületösszeg négyzetének a fele.   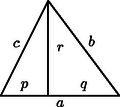2. Zsombori Gabriella (Csíkszereda, Márton Á. Gimn., IV. o.t.) megoldása a Stewart-tételen alapul. A tétel a 2. ábra jelöléseivel így fogalmazható meg: $b^{2}p+c^{2}q-a{r}^2=apq$. Bizonyítása megtalálható H. S. M. Coxeter‐S. L. Greitzer: Az újrafelfedezett geometria c. könyv 21‐22. oldalán. A tételt az 1. ábra $O{O}_2{O}_3$ háromszögére alkalmazva az (1) egyenletet kapjuk, amiből $x$ meghatározható. 3. Lobozár Ferenc második megoldásában az 1. ábra $B$ pontját választotta egy inverzió pólusául. Az inverzió alapkörének sugarát $d^2=BC\cdot BA=2r\left(2r+2R\right)=4r\left(r+R\right)$ összefüggéssel definiálta. Így a $B$ ponton átmenő két kör képe egy-egy egyenes lett, és a lényegesen egyszerűbb ábra alapján számolta ki a keresett sugarat.