Kezdőlap


Feladat:	F.3135	Korcsoport: 18-	Nehézségi fok: könnyű
Megoldó(k):	Varga Áron
Füzet:	1997/március, 164. oldal		PDF \| MathML
Témakör(ök):	Négyzetek, Kör geometriája, Terület, felszín, Szélsőérték-feladatok differenciálszámítás nélkül, Feladat
Hivatkozás(ok):	Feladatok: 1996/szeptember: F.3135

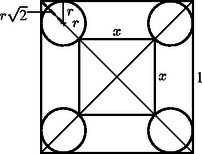
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Legyen a nagyobb négyzet oldala egységnyi, a kisebbiké $x$ , a körök sugara pedig $r$ . Az ábra alapján nyilvánvaló, hogy $\sqrt[]{2} = 2 (r \sqrt[]{2} + r) + x \sqrt[]{2}$ , amiből

\begin{matrix} r = \frac{\sqrt[]{2}}{2} \cdot \frac{1 - x}{\sqrt[]{2} + 1} = \frac{\sqrt[]{2}}{2} \cdot (\sqrt[]{2} - 1) (1 - x) . \end{matrix}

(1)

A sötét részek területének összege:

\begin{matrix} \begin{matrix} T (x) = x^{2} + 4 \cdot r^{2} \cdot π = x^{2} + 2 \cdot π \cdot {(\sqrt[]{2} - 1)}^{2} \cdot {(1 - x)}^{2}, \end{matrix} \end{matrix}

és így

\begin{matrix} \begin{matrix} (2) T (x) = (6 \cdot π - 4 \cdot π \cdot \sqrt[]{2} + 1) \cdot x^{2} + (8 \cdot π \cdot \sqrt[]{2} - 12 \cdot π) \cdot x + (6 \cdot π - 4 \cdot π \cdot \sqrt[]{2}) . \end{matrix} \end{matrix}

A feladat feltételei szerint:

\begin{matrix} \begin{matrix} (3) 0 < x < 1 és \\ (4) 4 r \leq 1. \end{matrix} \end{matrix}

Könnyen látható, hogy (2)-ben

x^{2}

együtthatója pozitív, ezért a (3) szerinti intervallumban lokális minimum lehetséges. Az

\begin{matrix} a x^{2} + b x + c = a {(x + \frac{b}{2 a})}^{2} + c - \frac{b^{2}}{4 a} \end{matrix}

azonosság alapján

T (x)

minimuma az

\begin{matrix} x_{0} = - \frac{8 π \cdot \sqrt[]{2} - 12 π}{2 \cdot (6 π - 4 π \cdot \sqrt[]{2} + 1)} \approx 0,5187 \end{matrix}

helyen lehetséges. Tekintve, hogy ezzel az értékkel ‐ (1)-ből

r

-et kiszámítva ‐ (3) és (4) teljesül,

x_{0}

-ban valóban minimum van.
Mivel a (3)-ban szereplő intervallum nyitott, maximum nem lesz.

Varga Áron (Budapest, Trefort Ágoston Kéttannyelvű Műsz. Szki. és Gimn., IV. o.t.)

dolgozata alapján