| Feladat: | F.3127 | Korcsoport: 16-17 | Nehézségi fok: átlagos |
| Megoldó(k): | Bérczi Gergely , Kocsis Zoltán , Rudolf Gábor , Terék Zsolt | ||
| Füzet: | 1997/január, 29 - 30. oldal |  PDF | PDF |  MathML MathML |
|
| Témakör(ök): | Kör geometriája, Lefedések, Hossz, kerület, Feladat | ||
| Hivatkozás(ok): | Feladatok: 1996/május: F.3127 | ||
|
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Először megmutatjuk, hogy két kör nem elég a lefedéshez. Egy 1-nél kisebb sugarú kör, ha két pontban metszi az egységkört, kerületének kevesebb, mint a felét tudja lefedni, hiszen a két kör metszéspontjainak távolsága kisebb az egységkör átmérőjénél. Ha viszont a két (egymást nem tartalmazó) körnek legfeljebb egy közös pontja van, akkor a kisebb kör legfeljebb egy pontot fed le.
2. Bérczi Gergely (Szeged, Ságvári E. Gyak. Gimn., II. o.t.) a következő általánosítási lehetőségre mutatott rá: Tekintsünk kör helyett egy tetszőleges korlátos és konvex síkidomot. -et hozzá középpontosan hasonló darab kicsinyített, nem feltétlenül egybevágó alakzattal szeretnénk lefedni. Mi lesz az pozitív egész legkisebb értéke? Feladatunk ennek az I. C. Gohberg és A. Sz. Markusz által 1960-ban kitűzött problémának speciális esete, amikoris az alakzat kör. Ekkor az minimuma . Az említett szerzők bebizonyították, hogy az szám legkisebb értéke paralelogramma esetén , minden egyéb korlátos konvex síkidomra . Az elemi, de mégis eléggé hosszadalmas bizonyítás megtalálható V. G. Boltjanszkij‐I. C. Gohberg: Alakzatok felbontása kisebb részekre című könyvének 53‐64. oldalán. A feladat második részére, vagyis hogy legalább mekkora lefedő alakzatokat kell alkalmaznunk, amikor a legkisebb, nem lehet ilyen egyszerűen válaszolni, a válasz függ a konvex síkidom alakjától. 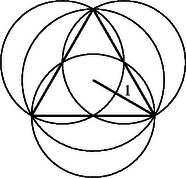 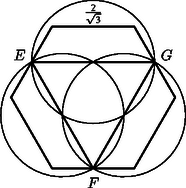 |