Feladat:	F.3123	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Frenkel Péter ,  Prause István ,  Terpai Tamás ,  Vörös Zoltán
Füzet:	1997/január, 26 - 27. oldal		PDF  |  MathML
Témakör(ök):	Másodfokú (és arra visszavezethető) egyenlőtlenségek, Térbeli ponthalmazok távolsága, Térgeometriai bizonyítások, Feladat
Hivatkozás(ok):	Feladatok: 1996/április: F.3123

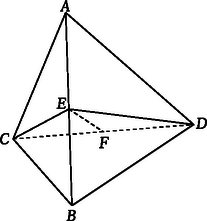
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.   I. megoldás. Legyen $AB$, illetve $CD$ felezőpontja $E$, illetve $F$. Ismeretes, hogy ha az $a$, $b$, $c$ oldalú háromszögben a $c$-hez tartozó súlyvonal $s_c$, akkor $2a^2+2b^2=c^2+4\cdot s_c^2$ (lásd pl. Geometriai feladatok gyűjteménye II. 291. feladat). Alkalmazzuk ezt az elfajuló háromszögre is érvényes összefüggést az $ABC$, $ABD$ és $ECD$ háromszögekre: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{cc}\hfill {\displaystyle 2A{C}^2+2B{C}^2}& {\displaystyle =A{B}^2+4C{E}^2\mathrm{,}}\hfill \\ \hfill {\displaystyle 2A{D}^2+2B{D}^2}& {\displaystyle =A{B}^2+4D{E}^2\mathrm{,}}\hfill \\ \hfill {\displaystyle 2C{E}^2+2D{E}^2}& {\displaystyle =C{D}^2+4E{F}^2\mathrm{.}}\hfill \end{array}}}\end{array}$ Az első két egyenlőség $\frac{1}{2}$-szeresét és a harmadik egyenlőséget összeadva, majd mindkét oldalból $2C{E}^2+2D{E}^2$-et kivonva: $\begin{array}{c}{\displaystyle A{C}^2+B{D}^2+A{D}^2+B{C}^2=A{B}^2+C{D}^2+4E{F}^2\mathrm{,}}\end{array}$ amiből $4E{F}^2\ge 0$ miatt következik a feladat állítása. Egyenlőség $EF=0$ esetén lesz, azaz, ha $AB$ és $CD$ felezik egymást. Ekkor $ACBD$ ‐ a pontoknak ebben a sorrendjében ‐ egy (esetleg elfajuló) paralelogramma csúcsai.  Frenkel Péter (Fazekas M. Főv. Gyak. Gimn., III. o.t.)   II. megoldás. Legyenek a tér egy tetszőleges pontjából az $A$, $B$, $C$, $D$ pontokhoz vezető vektorok $\text{a}$, $\text{b}$, $\text{c}$, $\text{d}$. Mivel pl. $A{C}^2={\left(\overrightarrow{AC}\right)}^2={\left(\text{c}-\text{a}\right)}^2$, a következö írható: $\begin{array}{c}{\displaystyle {\displaystyle \begin{array}{c}\hfill {\displaystyle A{C}^2+B{D}^2+A{D}^2+B{C}^2-A{B}^2-C{D}^2=}\\ \hfill {\displaystyle {\left(\text{c}-\text{a}\right)}^2+{\left(\text{d}-\text{b}\right)}^2+{\left(\text{d}-\text{a}\right)}^2+{\left(\text{c}-\text{b}\right)}^2-{\left(\text{b}-\text{a}\right)}^2-{\left(\text{d}-\text{c}\right)}^2={\left(\text{a}+\text{b}-\text{c}-\text{d}\right)}^2\ge \mathrm{0,}}\end{array}}}\end{array}$ ami a feladat állítását jelenti. Egyenlőség pontosan akkor lesz, ha $\text{a}+\text{b}-\text{c}-\text{d}=\text{0}$, vagyis $\text{a}-\text{c}=\text{d}-\text{b}$, tehát $ABCD$ egy (esetleg elfajuló) paralelogramma.  Prause István (Budapest, Piarista Gimn., III. o.t.)