Kezdőlap


Feladat:	F.3122	Korcsoport: 18-	Nehézségi fok: nehéz
Megoldó(k):	Bakos Péter , Barát Anna , Bérczi Gergely , Borsi Zsolt , Braun Gábor , Brezovich László , Czirok Levente , Fazekas Borbála , Frenkel Péter , Gueth Krisztián , Gyenes Zoltán , Gyukics Mihály , Hadházi Márton , Hans Zoltán , Huszár Gergely , Kiss Ádám , Lippner Gábor , Lolbert Tamás , Makai Márton , Mátrai Tamás , Méder Áron , Prause István , Salamon Gábor , Sánta Zsuzsa , Szabó Előd , Szabó Jácint , Szepesi Zoltán , Szobonya László , Terék Zsolt , Tóth Ádám , Tóth Éva , Tóth Péter , Tóth Zoltán Péter , Várkonyi Péter , Végh László
Füzet:	1997/január, 25 - 26. oldal		PDF \| MathML
Témakör(ök):	Háromszögek nevezetes tételei, Magasságvonal, Beírt kör, Hossz, kerület, Háromszögek hasonlósága, Feladat
Hivatkozás(ok):	Feladatok: 1996/április: F.3122

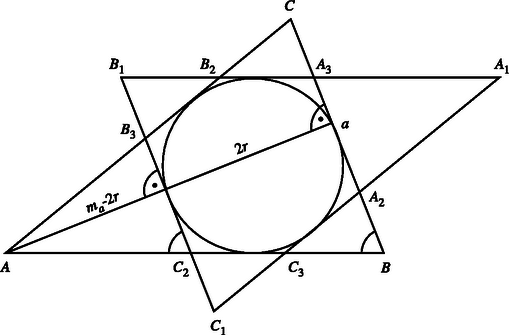
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre.

Az $A B C$ háromszög $A$ -ból induló magassága legyen $m_{a}$ , a beírt kör sugara $r$ . Használjuk az ábra további jelöléseit. Mivel $C_{2} B_{3} ‖ B C$ , az $A C_{2} B_{3}$ háromszög és az $A B C$ háromszög hasonlóak. Ezért $\frac{C_{2} B_{3}}{a} = \frac{m_{a} - 2 r}{m_{a}}$ , amiből $C_{2} B_{3} = a (1 - \frac{2 r}{m})$ . Ismeretes, hogy $r = \frac{t}{s} = \frac{a \cdot m_{a}}{2 s}$ , és így $\frac{2 r}{m_{a}} = \frac{a}{s}$ . Ezért $C_{2} B_{3} = a - \frac{a^{2}}{s}$ .
Hasonlóan $A_{2} C_{3} = b - \frac{b^{2}}{s}$ , és $B_{2} A_{3} = c - \frac{c^{2}}{s}$ . A hatszög középpontosan szimmetrikus, ezért kerülete:

\begin{matrix} K = 2 (C_{2} B_{3} + A_{2} C_{3} + B_{2} A_{3}) = 2 (a + b + c - \frac{a^{2} + b^{2} + c^{2}}{s}) . \end{matrix}

Azt kell bebizonyítanunk, hogy

2 (a + b + c - \frac{a^{2} + b^{2} + c^{2}}{s}) \leq \frac{2 (a b + b c + c a)}{a + b + c}

. Némi számolás után azt látjuk, hogy ez ekvivalens a

0 \leq {(a - b)}^{2} + {(b - c)}^{2} + {(c - a)}^{2}

egyenlőtlenséggel, ami nyilván igaz.
Egyenlőség pontosan akkor áll fenn, ha a háromszög szabályos.

Bérczi Gergely Szeged, Ságvári E. Gimn., II.o.t.

Szabó Jácint Győr, Révai M. Gimn., III.o.t.

Megjegyzés. Legyen a hatszög területe

T

és kerülete

K

, a háromszögé

t

, illetve

k

. Szabó Jácint megállapította, hogy

T = t (2 - \frac{a^{2} + b^{2} + c^{2}}{s^{2}})

, továbbá

\frac{T}{t} = \frac{K}{k} \leq \frac{2}{3}

. Az utóbbi relációban egyenlőség pontosan akkor lesz, ha a háromszög szabályos. Ez pl. azt is jelenti, hogy a hatszög akkor fedi le a háromszög területének legnagyobb hányadát ‐ számszerűen a kétharmadát ‐ ha a háromszög egyenlő oldalú.