|
| Feladat: |
F.3121 |
Korcsoport: 18- |
Nehézségi fok: nehéz |
| Megoldó(k): |
Bakos Péter , Barát Anna , Bérczi Gergely , Braun Gábor , Frenkel Péter , Gál Tamás , Gerő Tamás Miklós , Gyukics Mihály , Jeszenszky Gyula , Kiss Ádám , Koncz Imre , Léka Zoltán , Lippner Gábor , Lolbert Tamás , Makai Márton , Nagy Margit , Nyakas Péter , Prause István , Réfi Veronika , Rozmán András , Sánta Zsuzsa , Szabó Előd , Szabó Jácint , Szepesi Zoltán , Szita István , Szobonya László , Terpai Tamás , Tóth Péter , Tóth Zoltán Péter , Várkonyi Péter |
| Füzet: |
1997/január,
24 - 25. oldal |
 PDF | PDF |  MathML MathML |
| Témakör(ök): |
Háromszögek nevezetes tételei, Terület, felszín, Szögfüggvények, síkgeometriai számítások, Mértani közép, Feladat |
| Hivatkozás(ok): | Feladatok: 1996/április: F.3121 |
|
|
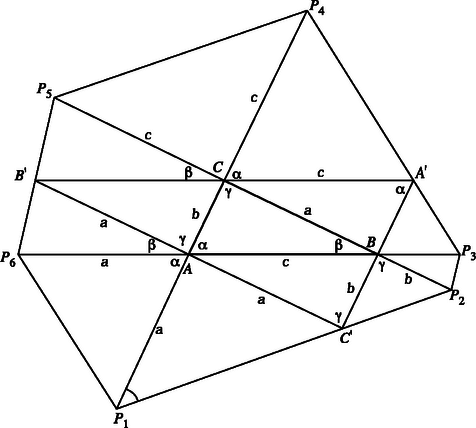
A szöveg csak Firefox böngészőben jelenik meg helyesen. Használja a fenti PDF file-ra mutató link-et a letöltésre. Jelöljük a háromszög adatait a
szokásos módon, az oldalakat , , -vel, stb. Használjuk az ábra további jelöléseit. Tükrözzük pl. a pontot az oldal felezőpontjára, a tükörkép legyen . Megmutatjuk, hogy illeszkedik -re. A feltételekből következik, hogy , ezért a . A
tükrözés következtében a -val jelölt szögek egyenlők, ezért a háromszög csúcsánál lévő szöge is , továbbá révén ez a háromszög is egyenlő szárú. Ezért . Azt kaptuk, hogy , és nyilván és a egyenesek ugyanabban a félsíkjában vannak, ezért illeszkedik -re. Hasonlóan látható, hogy illeszkedik -re, pedig -ra. Eddigi megállapításainkból következik, hogy az háromszög területe -szerese az háromszög területének.
A hatszög területét úgy fogjuk kiszámolni, hogy az háromszög területéhez hozzáadjuk még az ábrán jól látható 3‐3 , és csúcsú egyenlő szárú háromszög területét. Így azt kell igazolni, hogy , vagyis . Fölhasználva, hogy pl. , azt kell bizonyítanunk, hogy | |
azaz Mivel az , , számok mértani közepe ugyanaz, mint a , , számoké, ez utóbbi egyenlőtlenségünk a számtani és mértani közép, valamint a mértani és harmonikus közép közötti egyenlőtlenség alapján biztosan fennáll. Egyenlőség pontosan akkor lesz, ha .
| Lolbert Tamás Szombathely, Nagy L. Gimn., IV.o.t. |
Megjegyzés. Makai Márton (Debrecen, Fazekas M. Gimn., IV. o.t.) a feladatot úgy általánosította, hogy a háromszög csúcsaitól a megfelelő oldalak -szorosait mérte föl. Megmutatta, hogy az így keletkező hatszög területe a háromszög területének legalább -szerese.
|
|
 PDF |
PDF |  MathML
MathML